CTMU FR

CTMU — Le Modèle Théorique-Cognitif de l’Univers : Un nouveau type de théorie de la réalité

par Christopher Michael Langan, © 2002

Abstract : Dans la mesure où la science est observationnelle ou perceptuelle par nature, l’objectif de fournir un modèle et un mécanisme scientifiques pour l’évolution de systèmes complexes nécessite ultimement une théorie de la réalité qui la supporte, dont la perception elle-même est le modèle (ou cartographie théorie-à-univers). Lorsque l’information est la monnaie d’échange abstraite de la perception, une telle théorie doit incorporer la théorie de l’information tout en élargissant le concept d’information à un auto-traitement réflexif afin de parvenir à une description intrinsèque (autonome) de la réalité. Cette extension est associée à une formulation limitative de la théorie des modèles identifiant la réalité mentale et physique, aboutissant à une théorie de la réalité auto-génératrice réflexive, auto-modélisante, identique à son univers au niveau syntactique. Par la nature même de sa dérivation, cette théorie, le Modèle Théorique-Cognitif de l’Univers ou CTMU, peut être considérée comme une extension réalité-théorique supertautologique de la logique. Unissant la théorie de la réalité à une forme avancée de la théorie du langage informatique, le CTMU décrit la réalité comme un langage Auto-Configurant Auto-Traitant ou SCSPL, un langage intrinsèque réflexif caractérisé non seulement par l’autoréférence et l’autodéfinition récursive, mais aussi par la pleine auto-configuration et l’auto-exécution (fonctionnalité de lecture-écriture réflexive). La réalité SCSPL incarne un monisme à double aspect consistant en une infocognition, une information auto-transductrice résidant dans des éléments auto-reconnaissants SCSPL appelés opérateurs syntactiques. Le CTMU s’identifie lui-même à la structure de ces opérateurs et donc à la syntaxe distributive de son univers SCSPL auto-modélisant, y compris la grammaire réflexive selon laquelle l’univers s’affine à partir de la télèse non bornée ou UBT, un domaine primordial de potentiel infocognitif libre de contrainte informationnelle. Sous la direction d’un principe anthropique limitant (intrinsèque) appelé Principe Télique, le SCSPL évolue par récursion télique, configurant conjointement la syntaxe et l’état tout en maximisant un paramètre d’auto-sélection généralisé et en s’ajustant à la volée à des conditions internes librement variables. Le SCSPL relie l’espace, le temps et l’objet aux moyens de dualité conspansive et de conspansion, un processus grammatical-SCSPL présentant une alternance entre deux phases d’existence associées à la conception et à l’actualisation et liées à la dualité onde-particule familière de la mécanique quantique. En distribuant la phase de conception de la réalité sur la phase d’actualisation, l’espace-temps conspansif fournit également un mécanisme distribué pour la Conception Intelligente, contigu au principe restrictif de la sélection naturelle, un moyen basic de génération d’information et de complexité. Abordant l’évolution physique non seulement au niveau biologique mais aussi au niveau cosmique, le CTMU s’attaque aux carences et aux paradoxes les plus évidents associés aux modèles de réalité discrets et continus classiques, y compris la directionnalité temporelle et l’accélération de l’expansion cosmique, tout en préservant pratiquement tous les avantages majeurs des paradigmes mathématiques et scientifiques actuels.

Introduction

Parmi les développements scientifiques récents les plus intéressants il y a, la Théorie de la Complexité, la théorie des systèmes auto-organisants, et l’incarnation moderne de la Théorie de la Conception Intelligente, qui étudie la profonde relation entre l’auto-organisation et la biologie évolutionnaire dans un contexte scientifique non préventivement fermé à la causalité téléologique. Contre le réductionnisme physique traditionnel des sciences dures, la théorie de la complexité a donné naissance à une nouvelle tendance, le réductionnisme informationnel, selon laquelle le fondement de la réalité n’est pas matière et énergie, mais information. Malheureusement, cette nouvelle forme de réductionnisme est aussi problématique que l’ancienne. Comme l’écrit le mathématicien David Berlinski à propos des aspects matériels et informationnels de l’ADN : « Nous savons ce qu’est l’ADN: c’est une macromolécule et donc un objet matériel. Nous savons très bien ce que cela donne: apparemment tout. Les deux côtés de cette équation sont-ils en équilibre ? ». Plus généralement, Berlinski fait remarquer que, puisque l’information contenue dans une chaîne d’ADN ou de protéine ne peut affecter la dynamique matérielle de la réalité sans être lue par un transducteur matériel, l’information n’a pas de sens sans matière.1

La relation entre réductionnisme physique et informationnel est révélatrice, car elle reflète directement le dualisme esprit-matière Cartésien, source de plusieurs siècles de controverses philosophiques et scientifiques sur la nature de la réalité profonde.2 Tant que la matière et l’information restent séparées, les spécialistes considérant l’un comme primaire et reléguant tacitement l’autre au statut secondaire, le dualisme reste en vigueur. Dans cette mesure, l’histoire ne fait que se répéter; là où l’esprit et la matière se disputaient autrefois le statut principal, la matière concrète rivalise maintenant avec des informations abstraites représentant de manière abstraite la matière et ses relations étendues. Mais tandis que l’abstraction formelle et la descriptivité de l’information semblent donner un compromis louable entre esprit et matière, le commentaire de Berlinski montre son insuffisance en tant que substitut conceptuel. Ce qui est maintenant requis est ce qui l’a été tout du long : un cadre conceptuel dans lequel la relation entre l’esprit et la matière, la cognition et l’information, est explicitée. Ce cadre doit non seulement permettre d’achever la dissolution constante progressive du diviseur cartésien esprit-matière, mais également de construire un pont logique praticable au-dessus du fossé explicatif résultant.

Mathématiquement, le cadre théorique de la Conception Intelligente se compose de certains principes définitifs régissant l’application de la complexité et de la probabilité à l’analyse de deux attributs essentiels des phénomènes évolutionnaires, la complexité irréductible3 et la complexité spécifiée4. D’une part, étant donné que les mathématiques de probabilité doivent être interprétées causalement pour avoir une signification scientifique et que les probabilités sont donc expressément relativisées par rapport à des scénarios de causalité spécifiques, il est difficile d’attribuer des probabilités définies à des états évolutionnaires dans un modèle ne prenant pas en charge la reconstruction et l’analyse détaillées des voies causales spécifiques. D’autre part, poser « l’improbabilité absolue » d’un état évolutionnaire implique ultimement la spécification d’un modèle absolu (global intrinsèque) par rapport auquel il est possible de déterminer des écarts probabilistes absolus. Quelques réflexions suffisent pour nous informer de certaines de ses propriétés : il doit pouvoir être déduit rationnellement de principes a priori et essentiellement tautologiques par nature, il doit en quelque sorte identifier matière et information, et doit éliminer le fossé explicatif entre les aspects mentaux et physiques de la réalité. En outre, conformément au nom de ce qui doit être modélisé, il doit intégrer de manière significative les concepts d’intelligence et de conception, décrivant l’univers comme un système intelligemment auto-conçu et auto-organisé.

Comment est-ce fait ? En un mot, avec le langage. Cela ne signifie pas simplement que le langage devrait être utilisé comme un outil pour analyser la réalité, car cela a déjà été fait d’innombrables fois avec des degrés variés de succès. Cela ne signifie pas non plus que la réalité devrait être considérée comme un langage machine fonctionnant dans une sorte de vaste ordinateur. Cela signifie, utiliser la langue comme un paradigme mathématique en soi. De toutes les structures mathématiques, le langage est la plus générale, la plus puissante et la plus nécessaire. Non seulement chaque théorie formelle ou fonctionnelle de science et des mathématiques est par définition une langue, mais la science et les mathématiques, dans leur ensemble et leur somme, sont des langages. Tout ce qui peut être décrit ou conçu, y compris toute structure, processus ou loi, est isomorphe à une description ou définition et est donc qualifiable en tant que langage, et chaque créature sensible affirme constamment la structure linguistique de la nature en exploitant l’isomorphisme syntactique pour percevoir, conceptualiser et se référer à elle. Même la cognition et la perception sont des langages basés sur ce que Kant aurait pu appeler « syntaxe phénoménale ». Avec la logique et les mathématiques parmi ses ingrédients syntactiques les plus fondamentaux, le langage définit la structure même de l’information. C’est plus qu’une vérité empirique; c’est une nécessité rationnelle et scientifique.

Le fait que les lois de la nature soient un langage est particulièrement intéressant pour les scientifiques des sciences naturelles. Dans une certaine mesure, la nature est régulière; les modèles de base ou les aspects généraux de la structure en fonction desquels elle est appréhendée, qu’ils aient été identifiés de manière catégorique ou non, sont ses « lois ». L’existence de ces lois est donnée par la stabilité de la perception. Parce que ces modèles répétitifs ou lois universelles décrivent simultanément plusieurs instances ou états de la nature, ils peuvent être considérés comme des « instructions » distribuées à partir desquelles les auto-instanciations de la nature ne peuvent pas dévier; ainsi, ils forment un « langage de contrôle » à travers lequel la nature régule ses auto-instanciations. Ce langage de contrôle n’est pas du type habituel, car il est en quelque sorte intégré au tissu même de la réalité et semble outrepasser les limites connues des systèmes formels. De plus, il est profondément réflexif et autonome en ce qui concerne les opérations de configuration, d’exécution et de lecture-écriture. Seuls quelques-uns des audacieux ont été disposés à réfléchir à la manière dont cela pourrait fonctionner… à demander où les lois pourraient en réalité résider, comment elles pourraient être exprimées et mises en œuvre, pourquoi et comment elles sont apparues et comment leur consistance et leur universalité sont maintenues. Bien que ces questions présentent clairement un grand intérêt scientifique, la science seule est logiquement insuffisante pour y répondre; un nouveau cadre explicatif est nécessaire. Cet article décrit ce que l’auteur considère comme le cadre le plus prometteur dans les termes les plus simples et les plus directs possibles.

Sur une note d’indulgence, il a toujours été réconfortant de croire que les méthodes empiriques-mathématiques classiques hybrides de la physique et de la cosmologie suffiront à révéler le véritable cœur de la nature. Cependant, de nombreux signaux indiquent qu’il est peut-être temps de tenter une nouvelle approche. Avec les vrais croyants ne se laissant pas intimider par les limitations explicatives (mathématiquement factuelles) des anciennes méthodes, nous devons bien sûr faire preuve d’empathie; il est difficile de remettre en question ses investissements antérieurs quand on a déjà investi toute la foi que l’on a. Mais la science et la philosophie ne progressent pas en considérant leurs investissements passés comme une fin en soi; l’objet est toujours de préserver ce qui a de la valeur dans les méthodes anciennes tout en joignant de nouvelles méthodes qui affinent leur signification et élargissent leurs horizons. La nouvelle approche que nous allons explorer dans cet article, qui pourrait être décrite de façon pittoresque comme « la théorie de la réalité est liée à la théorie du langage et elles engendrent une synthèse », présente l’avantage de laisser virtuellement intact l’image actuelle de la réalité. Elle crée simplement une image miroir logique de l’image actuelle (son double conspansif), fusionne les moitiés symétriques de l’image résultante et tente d’extraire des implications significatives. La science telle que nous la connaissons est ainsi peu modifiée en contrepartie de ce qui peut, si le destin nous sourit, se révéler être de vastes gains en profondeur, en signification et en pouvoir explicatif.

Et sur cette note, je vous remercie de votre aimable attention et vous souhaite un voyage fructueux.

Théories, modèles et fausses dichotomies

Il est presque devenu embarrassant de faire remarquer que la science est en état de crise… non pas parce que c’est erroné, mais parce c’est devenu un cliché trop souvent accompagné de peu ou pas d’éclaircissement correcteur. Malgré toutes les réalisations magnifiques de la science, ses ambitions grandioses ont réussi depuis longtemps à éprouver ses modèles traditionnels et ses principes d’organisation au-delà de leurs limites explicatives. À la recherche d’explications toujours plus profondes et plus larges, la science a atteint le point où elle ne peut plus nier l’existence de difficultés conceptuelles insolubles conduisant aux insuffisances explicatives de ses modèles conceptuels fondamentaux de la réalité. Cela a engendré une nouvelle discipline connue sous le nom de théorie de la réalité, l’étude de la nature de la réalité dans son sens le plus large. L’objectif général de la théorie de la réalité est de fournir de nouveaux modèles et de nouveaux paradigmes aux termes desquels la réalité peut être comprise, et la consistance de la science être restaurée à mesure qu’elle s’approfondit et élargit son étendue.

La théorie de la réalité dominante compte parmi ses foyers les plus chauds l’interprétation de la théorie quantique et sa réconciliation avec la physique classique, l’étude de la conscience subjective et ses relations avec la réalité matérielle objective, la réconciliation entre science et mathématiques, la théorie de la complexité, la cosmologie et les branches connexes de science, mathématiques, philosophie et théologie. Mais dans un sens intégrée, elle est actuellement dans un mode exploratoire, occupée à la recherche d’un cadre conceptuel général dans lequel développer une théorie et un modèle de réalité plus spécifiques, capables de résoudre les paradoxes et les inconsistances conceptuelles qui affectent ses différents domaines d’intérêt (où un modèle est techniquement défini comme une interprétation valide d’une théorie dans son univers de référence). En raison de la portée universelle de la théorie de la réalité, elle est sujette à des exigences uniques et rarement reconnues; par exemple, puisqu’il s’agit par définition d’une théorie universelle de tout ce qui est réel, elle doit par définition contenir ses règles d’interprétation du monde réel. C’est-à-dire que la théorie de la réalité doit contenir son propre modèle et lui affecter sa propre cartographie auto-interprétative, et elle doit se conformer aux implications de cette exigence. Cette capacité « d’auto-modélisation » est un critère principal du cadre requis.

Les rangs des théoriciens de la réalité incluent des chercheurs de presque toutes les disciplines scientifiques. Au fur et à mesure que les sciences physiques se sont investies davantage dans une vision quantique mécanique de la réalité et que la science en général est devenue plus éprise et dépendante de la simulation sur ordinateur en tant qu’outil expérimental, le modèle de continuum traditionnel des physiques classique a progressivement perdu du terrain au profit de nouvelles classes de modèles pour lesquels les concepts d’information et de calcul sont essentiels. Appelés « modèles discrets », ils décrivent la réalité en termes de bits, quanta, événements quantiques, opérations de calcul et autres unités discrètes, récursivement liées. Alors que les modèles de continuum sont basés sur la notion de continuum, un tout extensible unifié avec un ou plusieurs paramètres de distance pouvant être subdivisés à l’infini de manière à ce que deux points distincts soient séparés par un nombre infini de points intermédiaires, les modèles discrets se distinguent par une reconnaissance réaliste du fait qu’il est impossible de décrire ou de définir un changement ou une séparation d’une manière qui n’implique pas un saut fini soudain dans un paramètre.

Malheureusement, les avantages des modèles discrets, qui font l’objet d’une attention de plus en plus sérieuse de la part des communautés scientifiques et philosophiques, sont contrebalancés par certaines lacunes fondamentales. Non seulement ils présentent des problèmes de mise à l’échelle et de non-localité associés à leur « matériel d’affichage », mais ils sont inadéquats, à eux seuls, pour générer l’infrastructure conceptuelle nécessaire pour expliquer le support, le périphérique ou le tableau dans lequel ils évoluent, ou leurs états initiaux et leur programmation de transition d’état. De plus, ils restent ancrés dans le matérialisme, l’objectivisme et le dualisme Cartésien, qui se sont tous révélés être des obstacles au développement d’une explication complète de la réalité. Le matérialisme exclut arbitrairement la possibilité que la réalité ait un aspect non matériel significatif, l’objectivisme exclut arbitrairement la possibilité que la réalité ait un aspect subjectif significatif, et bien que le dualisme Cartésien n’exclue techniquement aucun des deux, il nie arbitrairement que les aspects mentaux et matériels, ou subjectifs et objectifs, de la réalité partagent une substance commune.5

On pourrait presque avoir l’impression que les deux seuls choix possibles sont le modèle classique, auquel la théorie quantique a été fixée avec à peu près le même degré de cohérence que des bois sur un lièvre, et les nouveaux modèles discrets, qui se veulent plus alignés avec la théorie quantique mais échouent sur le bas-côté de la route vers un nouveau type de cosmologie quantique qu’ils semblent promettre de façon insolite. Car de telles affirmations présentent une ironie évidente : la réalité classique est précisément celle sur laquelle sont définies l’information et le calcul ! Comme la réalité classique elle-même, une entité bien définie incapable de rendre compte de sa propre genèse, l’information et le calcul sont des aspects bien définis et non auto-génératifs de la réalité telle qu’elle se présent observationnellement à nous à un stade avancé de son existence. Ils invitent donc aux mêmes questions que la réalité classique : comment et par quoi ont-ils été définis et générés à l’origine ? Sans une réponse à cette question, on ne gagne pas grand-chose à remplacer une sorte de réalité par l’autre.

Certains ont peut-être ressenti, alors qu’ils regardaient l’histoire des grandes théories et des nouveaux paradigmes se dérouler ces dernières années, comme s’ils étaient obligés de regarder la même série, ou de lire le même roman, mille fois en successions fastidieuses sans rien de plus qu’une révision mineure occasionnelle de l’intrigue ou des personnages. Cependant, il y a une troisième alternative qui est jusqu’ici restée en arrière-plan. Elle fournit exactement ce qui est requis à la lumière de toute thèse et antithèse : une synthèse. Cette synthèse donne une nouvelle classe de modèle(s)6 préservant les meilleures caractéristiques de la thèse et de l’antithèse, le continuum et le quantum, en les unissant par le biais de principes généraux et de préférence auto-évidents. Cet article présente cette nouvelle classe à travers un seul exemple, le Modèle Théorique-Cognitif de l’Univers (CTMU).

Déterminisme, indéterminisme et troisième option

Comme les mathématiques, la science et la philosophie d’où ils découlent, le continuum classique et les modèles discrets modernes de la réalité autorisent généralement exactement deux modes de déterminismes : la causalité externe et l’acausalité ou « hasard ». Étant donné un objet, un événement, un ensemble ou un processus, on suppose généralement qu’il s’est produit d’une ou des deux manières suivantes : (1) son existence est due à quelque chose d’antérieur et d’extérieur à lui; (2) il est sans cause et a surgi spontanément et inutilement d’une manière à-partir-de-rien, sortie-du-chapeau, comme par magie. Une hypothèse similaire est faite en ce qui concerne son comportement : soit il est contrôlé par des lois qui sont invariantes à son égard et donc existentiellement externes à celui-ci (même si elles le contrôlent par sa structure et ses propriétés intrinsèques), ou bien il se comporte d’une manière totalement aléatoire et incontrôlée. Cela a donné lieu à une dichotomie : déterminisme versus hasard, ou une absence totale de causalité versus causalité par des lois ultimement indépendantes de l’entité déterminée.

Déterminisme et indéterminisme… à première vue, il ne semble pas y avoir de terrain commun. Les événements sont soit causalement liés, soit ils ne le sont pas, et s’ils ne le sont pas, alors l’avenir semble totalement indépendant du passé. Soit nous utilisons la causalité pour relier les points et dresser une image cohérente du temps, soit nous nous contentons d’une diffusion aléatoire de points indépendants sans motif spatial ou temporel et donc sans signification. Au risque d’un euphémisme, les effets philosophiques de cette dichotomie supposée ont été extrêmement corrosifs. Aucun univers qui existe ou évolue strictement en fonction d’un déterminisme externe, du hasard ou d’une alternance des deux ne peut offrir beaucoup de sens. Là où la liberté et la volonté sont hors de propos, il en va de même pour la majeure partie de l’expérience et de l’individualité humaines.

Mais après tout, il y a une autre possibilité : l’autodéterminisme. L’autodéterminisme est comme un bord détourné séparant les pôles de la dichotomie précédente… un bord réflexif, et donc fermé, dont la formation n’implique ni lois préexistantes ni structure externe. Il s’agit donc du type d’attribution causale approprié pour un système parfaitement autonome. L’autodéterminisme est un concept profond mais subtil, dû en grande partie au fait que, contrairement au déterminisme ou au hasard, il est une source de sens authentique. Lorsqu’un système détermine sa propre composition, ses propriétés et son évolution indépendamment de lois ou des structures externes, il peut déterminer son propre sens et s’assurer de son auto-configuration que ses habitants y sont impliqués de manière cruciale.

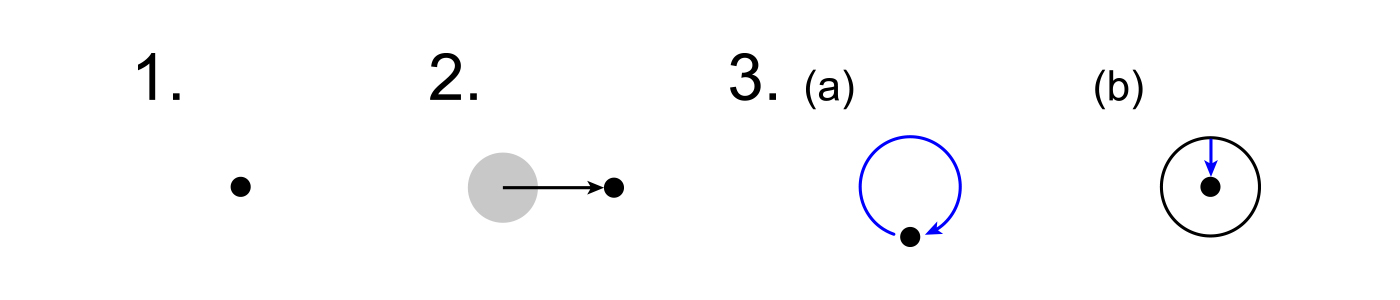
Diagramme 1 : 1. Indéterminisme 2. Déterminisme externe 3a. Autodéterminisme 3b. Autodéterminisme intrinsèque (l’aspect effectif de l’objet ou de l’événement a simplement été déplacé à l’intérieur de l’aspect causal, permettant l’internalisation de la flèche bleue du déterminisme et rendant la causalité endomorphique.)

Si le déterminisme correspond à une flèche de causalité pointant vers un événement à partir d’un support environnant, l’indéterminisme ne correspond à aucune flèche (acausalité) et l’autodéterminisme à une flèche bouclée ou à un complexe de flèches impliquant une rétroaction quelconque. Mais la rétroaction cybernétique, qui implique des informations transmises aux contrôleurs et aux entités régulées via un support conducteur ou transmissif, n’a pas de sens lorsque de telles entités n’existent pas déjà et qu’aucun protocole sensoriel ou actionnant n’a encore été fourni. En ce qui concerne l’origine de tout système autodéterminant, parfaitement autonome, la rétroaction d’information est de nature ontologique et est donc plus que cybernétique. En conséquence, la rétroaction ontologique porte la description de « précybernétique » ou « métacybernétique ». En effet, en raison de leurs relations particulièrement étroites, les théories de l’information, du calcul et de la cybernétique s’inscrivent dans le prolongement d’une extension convergente… une extension qui peut, dans un contexte de théorie de la réalité, jeter l’essentiel des bases d’une extension convergente de tout ce qui est couvert par leurs formalismes respectifs.7

La rétroaction ordinaire, décrivant l’évolution des systèmes mécaniques (et avec un peu moins de succès, biologique), est cyclique ou récursif. Le système et ses composants font régulièrement appel à des structures internes, à des routines et à des mécanismes d’actionnement pour acquérir des entrées, générer les informations internes correspondantes, les communiquer en interne et les traiter, et évoluer vers les états appropriés en fonction des entrées et de la programmation. Cependant, lorsque l’objet consiste à décrire l’évolution d’un système d’un état dans lequel il n’y a aucune information ou programmation (syntaxe de traitement de l’information), un nouveau type de rétroaction est requis: la rétroaction télique.

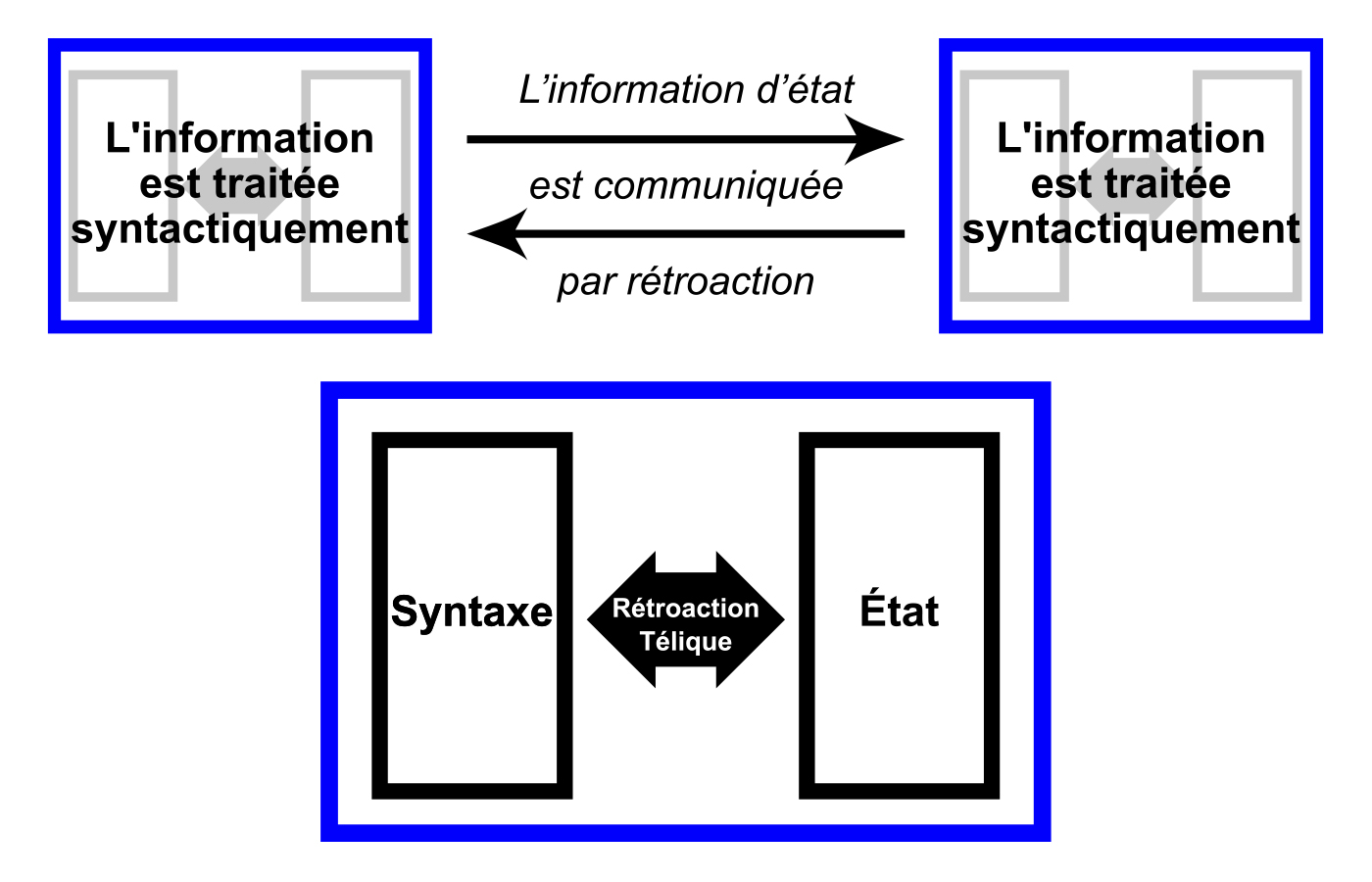
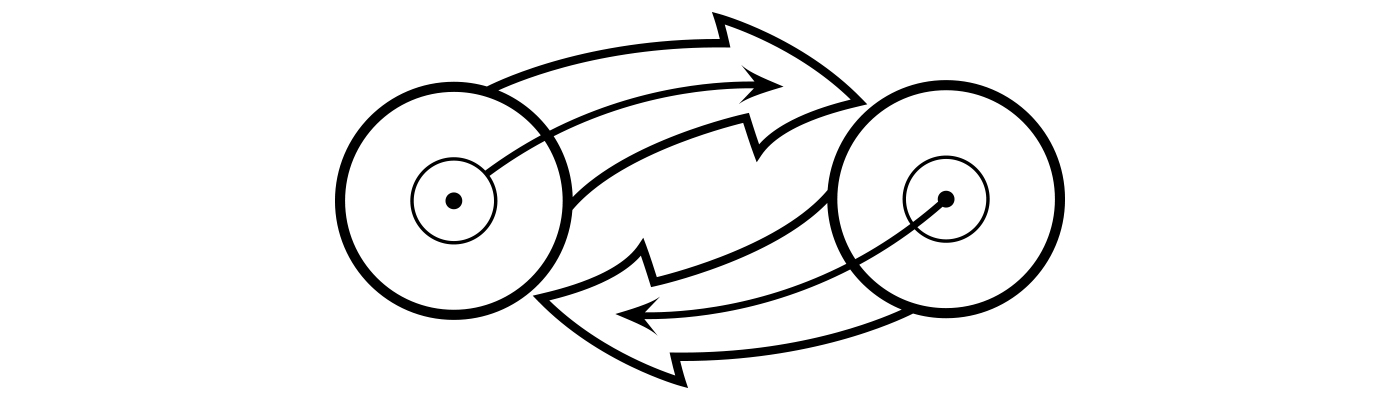
Diagramme 2 : Le diagramme supérieur illustre les rétroactions cybernétiques ordinaires entre deux transducteurs d’information qui échangent et agissent sur des informations reflétant leurs états internes. La structure et le comportement de chaque transducteur sont conformes à une syntaxe ou à un ensemble de règles structurelles et fonctionnelles qui déterminent son comportement pour une entrée donnée. Dans la mesure où chaque transducteur est soit déterministe, soit non déterministe (dans les limites d’une contrainte syntactique), le système est soit déterministe, soit « aléatoire jusqu’au déterminisme »; il n’y a pas de disposition pour l’auto-causation en dessous du niveau systémique. Le diagramme inférieur, qui s’applique aux systèmes cohérents d’auto-conception, illustre une situation dans laquelle la syntaxe et l’état sont plutôt déterminés en tandem conformément à une fonction d’utilité généralisée attribuant des valeurs différentielles, mais à l’échelle intrinsèque, à diverses relations syntaxe-état possibles. Une combinaison de ces deux scénarios est partiellement illustrée dans le diagramme supérieur par les ombres grises dans chaque transducteur.

La monnaie du rétroaction télique est un paramètre quantifiable d’auto-sélection, une utilité généralisée, une propriété généralisée de loi et d’état dans la maximisation de laquelle ils subissent un raffinement mutuel (notez que l’utilité généralisée est auto-descriptive ou autologue, définie intrinsèquement et rétroactivement dans le système, et « pré-informationnelle » dans le sens où elle n’attribue aucune propriété spécifique à un objet spécifique). À travers la rétroaction télique, un système s’auto-configure rétroactivement en appliquant réflexivement une « fonction d’utilité généralisée » à son potentiel existentiel interne ou à ses futurs possibles. En effet, le système s’amène à l’existence comme un moyen de communication intemporel entre son passé et son futur, selon lequel la loi et l’état, la syntaxe et le contenu informationnel, se génèrent et s’affinent mutuellement à travers le temps pour maximiser l’auto-utilité systémique. Cela définit une situation dans laquelle la véritable identité temporelle du système est un point d’équilibre temporel distribué, qui est à la fois entre et inclusif au passé et au futur. En ce sens, le système est intemporel ou atemporel.

Un système qui évolue au moyen de la récursion télique – et en fin de compte, chaque système doit être ou être incorporé dans un tel système en tant que condition d’existence – n’est pas simplement calculatoire, mais protocalculatoire. C’est-à-dire que son niveau de traitement principal configure son niveau de traitement secondaire (calculatoire et informationnel) par récursion télique. La récursion télique peut être considérée comme le mécanisme autodéterminant, non seulement de la cosmogonie, mais aussi comme une forme naturelle et scientifique de la téléologie.

Cependant, avant d’approfondir ces idées, assistons à une petite séance d’orientation basée sur la vision remarquablement pénétrante de John Archibald Wheeler, scientifique de renom et théoricien de la réalité, dont le nom est pratiquement synonyme de physique moderne.

L’avenir de la théorie de la réalité selon John Wheeler

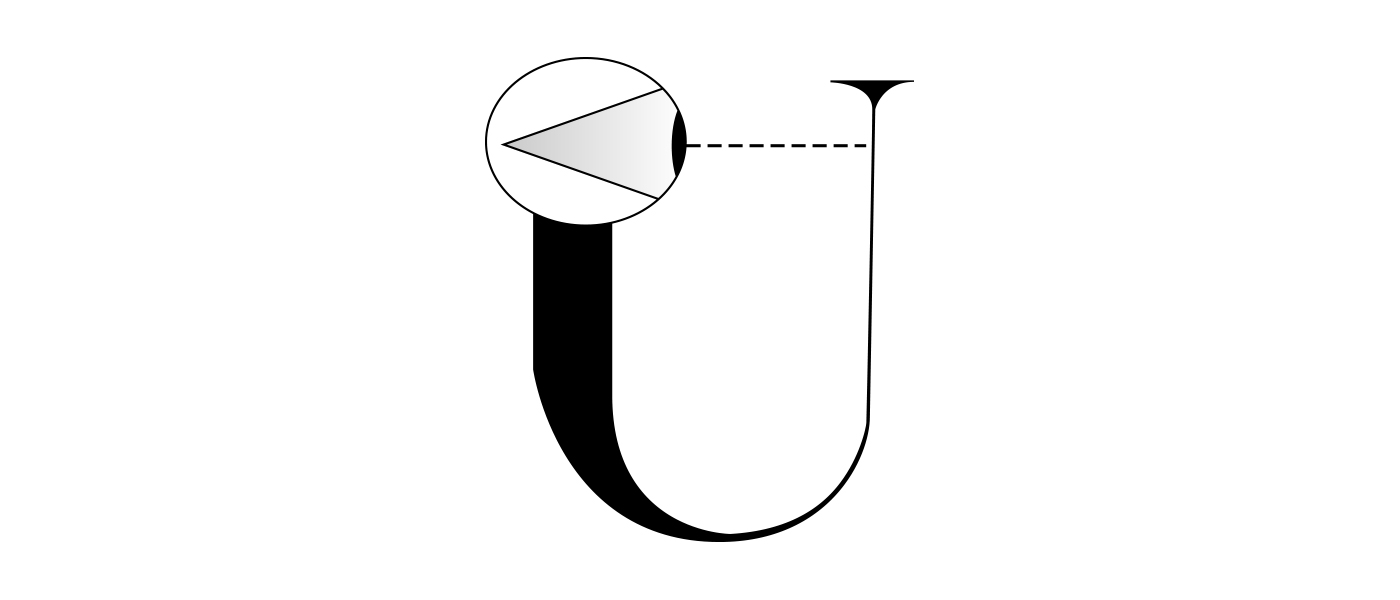
En 1979, le célèbre physicien John Wheeler, après avoir inventé l’expression « trou noir », en fit un bon usage philosophique dans le titre d’un article exploratoire intitulé Beyond the Black Hole8, dans lequel il décrit l’univers comme un circuit auto-excité. Le document inclut une illustration dans laquelle un côté d’une lettre majuscule U, représentant ostensiblement l’Univers, est doté d’un œil large et à l’air plutôt intelligent qui regarde attentivement l’autre côté, qu’il acquiert apparemment par l’observation en tant qu’information sensorielle. Grâce au placement, l’œil représente l’aspect sensoriel ou cognitif de la réalité, peut-être même un spectateur humain dans l’univers, tandis que la cible perceptuelle de l’œil représente l’aspect informationnel de la réalité. En vertu de ces aspects complémentaires, il semble que l’univers puisse dans un certain sens, mais pas nécessairement dans son usage courant, être décrit comme « conscient » et « introspectif »… peut-être même « infocognitif ».

Diagramme 3 : L’Univers en tant que circuit auto-excité. Cliquez pour l’animation [Diagramme adapté de Wheeler, J. A., « Beyond the Black Hole », dans Some Strangeness in the Proportion: A Centennial Symposium to Celebrate the Achievments of Albert Einstein, Woolf, H. (éd.), Addison-Welsley, 1980. p. 362.]

Wheeler, un représentant éminent et hautement compétent de ceux qui sont familiers des avantages et les inconvénients de nos modèles actuels de réalité, n’est pas parvenu à l’illustration donnée en tant que spéculation isolée. En conjonction avec plusieurs autres concepts de Wheeler, l’« Univers Participatif », la « Loi sans Loi » et le « It from Bit », le circuit auto-excité constitue un programme préliminaire, mais bien pensé, pour décrire l’univers physique. Selon son mandat, la véritable description de la réalité doit posséder deux caractéristiques nouvelles qui ne se retrouvent dans aucun paradigme dominant : (1) réflexivité structurelle et dynamique globale ou « circuit auto-excité », la perception faisant partie intégrante de la fonction d’auto-reconnaissance de la réalité ; (2) équivalence matière-information, identification (jusqu’à l’isomorphisme) de la réalité physique concrète avec l’information, monnaie abstraite de la perception. Ensemble, ces caractéristiques constituent une extension cosmologique de la cybernétique ou, de manière équivalente, une extension métacybernétique de la cosmologie.

Wheeler caractérise ces quatre concepts comme suit :

Le circuit auto-excité : Un univers participatif est un circuit auto-excité dans le sens où il implique en rétroaction (perceptuel, ontologique) les observateurs. C’est une « boucle logique » dans laquelle « la physique donne lieu à la participation de l’observateur; la participation de l’observateur donne lieu à l’information; et l’information donne naissance à la physique. »9

L’Univers Participatif : les processus cognitifs et perceptuels des observateurs font partie intégrante de la rétroaction auto-excitante de la réalité. Ceci est affirmé par le Principe Participatif (ou Principe Anthropique Participatif), que Wheeler décrit de manière informelle comme suit : « Plus fort que le Principe Anthropique est ce que je pourrais appeler le Principe Participatif. Selon celui-ci, nous ne pourrions même pas imaginer un univers qui ne contienne quelque part et pendant un certain temps des observateurs, car les propres matériaux de construction de l’univers sont ces actes d’observation-participation… Ce principe participatif prend pour fondement le point absolument central du quantum : aucun phénomène élémentaire n’est un phénomène tant qu’il ne s’agit pas d’un phénomène observé (ou inscrit) » [emphase ajoutée]. Notez qu’à un certain niveau de généralité, la dernière phrase identifie l’observation avec l’inscription et assimile donc implicitement la reconnaissance humaine et mécanique : « … un phénomène observé (ou inscrit) ». [Emphase de nouveau ajoutée].10

Loi Sans Loi / Ordre du Désordre: En résumé, rien ne peut être pris pour acquis en matière de cosmogonie. Selon les propres mots du professeur Wheeler: « Pour moi, la plus grande découverte à venir sera de trouver comment cet univers, né d’un Big Bang, a développé ses lois de fonctionnement. J’appelle cela « la Loi Sans Loi » [ou « l’Ordre du Désordre »]. (…) Imaginez l’univers avec toutes ses régularités et ses lois en train de naître de quelque chose de complètement désordonné, pêle-mêle et aléatoire… Si vous étiez le Seigneur qui construisait l’univers, comment l’auriez-vous fait ? Il est inspirant de lire la vie de Charles Darwin et de penser comment la division des règnes végétal et animal, toute cette myriade d’ordres, est née des miracles de l’évolution, de la sélection naturelle et de la mutation fortuite. Pour moi, c’est une indication merveilleuse que vous pouvez obtenir l’ordre en commençant par le désordre. »11

It From Bit : La réalité se construit et/ou se produit sous la forme d’informations résidant dans des événements quantiques. Comme le résume Wheeler dans son article Information, Physics, Quantum: The Search for Links, « … chaque quantité physique, chaque chose, tire sa signification ultime de bits, d’indications binaires oui-ou-non… ». Il aborde ensuite ce concept en détail en proposant trois questions, quatre « non » et cinq « indices » sur le caractère informationnel-quantique de la réalité. Les questions sont les suivantes : (1) Comment survient l’existence ? (2) Comment survient le quantum ? (3) Comment survient le « monde unique » composé de nombreux observateurs-participants ? Les non, pièges séduisants à éviter pour répondre aux trois questions, ne comprennent aucune tour de tortues, aucune loi, aucun continuum, et aucun espace ou temps. Et les indices, qui éclairent le chemin vers les vraies réponses, incluent la limite d’une limite est zéro; Pas de question ? Pas de réponse ! ; Le Principe Super-Copernicien; « La Conscience » (y compris les guillemets); et plus est différent.12

Nous allons maintenant donner un bref compte rendu de ces questions, précautions et indices.

Comment survient l’existence ? La portée ontologique et cosmologique de cette question est évidente; sous une forme ou une autre, elle a miné les philosophes depuis des temps immémoriaux. Tel qu’interprété par Wheeler, cela conduit à quatre conclusions inévitables. « (1) Le monde ne peut pas être une machine géante, gouvernée par un quelconque continuum de loi physique préétabli. (2) Au niveau microscopique, il n’existe pas d’espace ou de temps ou de continuum espace-temps. (3) La fonction de probabilité familière ou fonctionnelle, et l’équation d’onde ou équation d’onde fonctionnelle, de la théorie quantique standard fournissent de simples idéalisations de continuum et, en raison de cette circonstance, dissimulent la source d’information-théorique à partir de laquelle elles sont dérivées. (4) Aucun élément dans la description de la physique ne se montre aussi près d’être primordial que le phénomène quantique élémentaire, c’est-à-dire l’acte élémentaire-intermédiaire qui consiste à poser une question physique du type oui-ou-non et à obtenir une réponse ou, en bref, l’acte élémentaire de participation d’un observateur. Autrement dit, chaque grandeur physique, chaque chose, tire sa signification ultime de bits, d’indications binaires oui-ou-non, conclusion que nous résumons dans l’expression it from bit. »13

Comment survient le quantum ? Pourquoi l’univers est-il constitué d’événements quantiques apparemment propter hoc non déterministes, mais post hoc informationnels ? Comme le remarque Wheeler, « La physique quantique nécessite une nouvelle vision de la réalité » 14 Quelle est donc la relation logique exacte entre le quantum et la nouvelle vision de la réalité qu’elle exige ? Quelle est cette nouvelle vision et comment le quantum s’y intègre-t-il ?

Comment survient le « monde unique » parmi de nombreux observateurs-participants ? Dans la mesure où le terme « observateurs-participants » englobe les scientifiques et les autres êtres humains, cette question invite une interprétation quasi anthropologique. Pourquoi un univers composé d’observateurs distincts dont les programmes et les impératifs de survie sont parfois contradictoires devrait-il afficher une unité structurelle et nomologique ? Lorsque les observateurs sont capables de créer des événements dans la variété unitaire globale de leur univers commun, pourquoi ne le feraient-ils pas strictement pour eux-mêmes, chacun dans son propre univers, et jamais les deux ne se rencontreraient ? Lorsque le concept observateur-participant est généralisé pour inclure des systèmes non anthropiques de transduction d’informations, qu’est-ce qui maintient l’ensemble de ces systèmes dans une seule et même réalité ?

Aucune tour de tortues : Emprunté à William James, cet aphorisme signifie « pas de régression infinie vers des domaines et principes de causalité toujours antérieurs ». À cela, nous pourrions assimiler une version mise à jour d’un aphorisme bien connu, attribué à Harry Truman : « Le pouvoir explicatif s’arrête ici », où ici fait référence à cette réalité que nous habitons et observons. Wheeler ajoute à cela une idée cruciale: « À l’infini, aucune autre alternative n’est évidente qu’une boucle, telle que : la physique donne lieu à la participation de l’observateur; la participation de l’observateur donne lieu à l’information; et l’information donne naissance à la physique »15. Seule une telle boucle ontologique est capable de former un collet suffisamment large et fort pour le ceinturage théorique de la réalité; la tâche à accomplir est donc de trouver un moyen de le fabriquer et un support par lequel le manier.

Aucune Loi : Comme le dit Wheeler, « L’univers doit être né… sans même un plan préexistant… seul un principe d’organisation qui ne serait aucune organisation du tout semblerait s’offrir à lui-même » 16. Ou pour réitérer: « Le monde ne peut pas être une machine géante, gouvernée par un quelconque continuum de loi physique préétabli. »

Aucun continuum : le vénérable continuum d’analyse et de mécanique est une chimère mathématique et physique. (Habituellement associé à l’ensemble des nombres réels, un continuum est un ensemble extensible unifié avec un paramètre de distance pouvant être subdivisé à l’infini de manière à ce que deux points distincts soient séparés par un nombre infini de points intermédiaires.) Comme le dit Wheeler: « Un demi-siècle de développement dans le domaine de la logique mathématique a clairement montré qu’il n’y avait aucune preuve à l’appui de la croyance en le caractère existentiel du continuum des nombres 17 ». Quelques nombres, par exemple les irrationnels tels que √2 ne peuvent pas être calculés avec précision et ne correspondent donc à aucun emplacement physiquement significatif sur une droite numérique ou une trajectoire physique; ils ont une existence uniquement abstraite.

Aucun espace ou temps : Encore une fois, « Au niveau microscopique, il n’existe pas d’espace ou de temps ou de continuum espace-temps ». Au niveau submicroscopique, le principe d’incertitude de Heisenberg transforme l’espace-temps en une « mousse quantique » apparemment chaotique, jetant le doute sur la connectivité de l’espace et son ordinalité. Wheeler cite Einstein dans une veine kantienne: « Le temps et l’espace sont des modes par lesquels nous pensons, et non des conditions dans lesquelles nous vivons », considérant ces modes comme pouvant être dérivés d’une théorie propre à réalité en tant que fonctions idéalisées d’un continuum idéalisé: « Nous n’introduirons le temps dans aucun compte-rendu profond de l’existence. Nous devons dériver le temps (et seulement le temps du continuum idéalisé). De même avec l’espace. »18

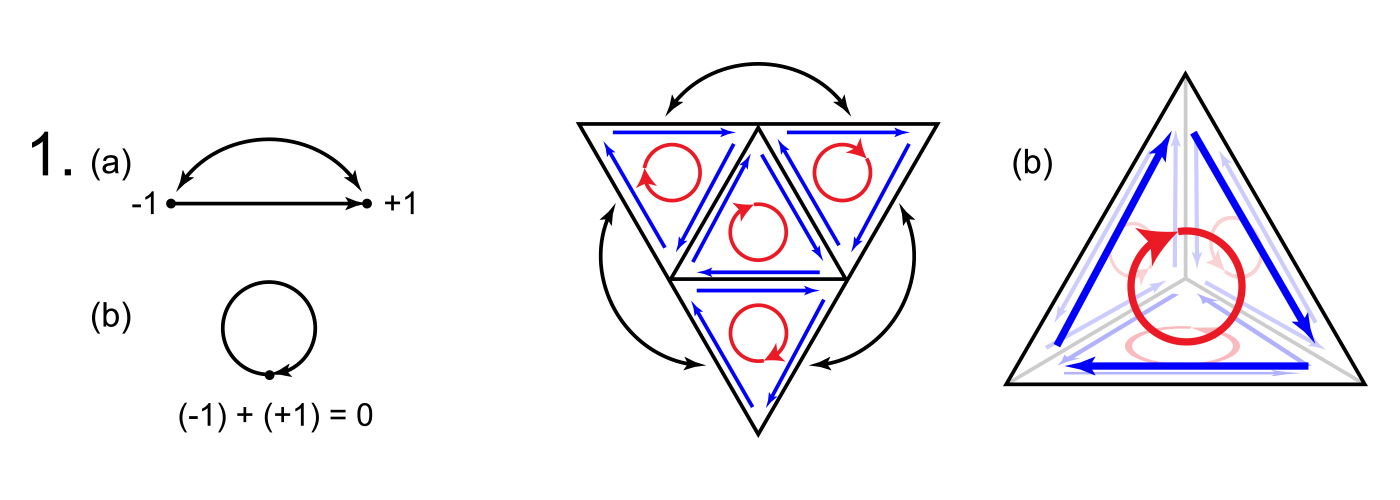
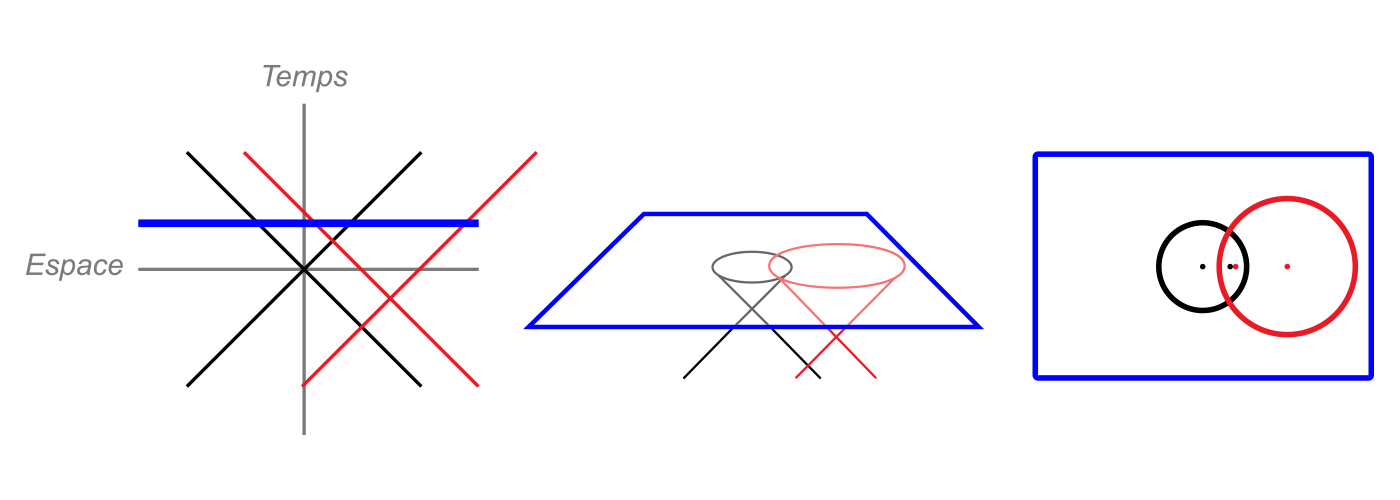
La limite d’une limite est zéro : En substance, cette notion intuitive de la topologie algébrique dit que les structures fermées incarnent un certain type de symétrie « auto-annulable ». Ceci peut être illustré en trois dimensions par un tétraèdre dont le « bord » simplicial incorpore ses quatre faces triangulaires équilatérales. Pour trouver le bord de ce bord, vous devez mesurer les arrêtes orientés dans le sens horaire – ou antihoraire – autour de chaque face, mesurant ainsi chaque arrête du tétraèdre deux fois dans des directions opposées. Étant donné que la somme des mesures s’annule maintenant à 0 à chaque arrête, le bord du bord du tétraèdre est égale à zéro. Cette propriété s’avère avoir de nombreuses applications en physique, en particulier dans la théorie des champs, en ce qui concerne « l’emprise » réciproque de la matière sur l’espace et de l’espace sur la matière (ou, de manière moins colorée, la relation entre l’espace et la matière). Dans la vision de Wheeler, son ubiquité « inspire l’espoir que nous allons un jour compléter les mathématiques de la physique et tirer le tout de rien, toute loi d’aucune loi » 19. Ainsi, il est étroitement lié à la loi sans loi et à la création dite ex nihilo.

Diagramme 4 : 1a : Le bord d’un segment de droite 1-dimensionnelle orientée est constitué de ses extrémités 0-dimensionnelles, qui séparent la ligne de son complément (l’espace qui l’entoure). Le point initial représente la « dette » requise pour démarrer la ligne et reçoit donc une valeur de -1, tandis que le point terminal représente le « paiement » pour compléter la ligne et reçoit une valeur de +1. Lorsque les points initial et terminal de la ligne sont identifiés comme indiqué par la flèche incurvée, il en résulte une ligne fermée délimitant un disque plan (1b). Comme les points d’extrémité coïncident maintenant, ils totalisent 0 et ne séparent plus la ligne de son complément; ainsi, le bord 0-dimensionnel du bord 1-dimensionnel du disque 2-dimensionnel est 0. 2a: Une zone triangulaire peut être décomposée en 4 zones triangulaires plus petites. L’introduction d’une orientation uniforme (dans ce cas, dans le sens horaire) par rapport aux zones (flèches rouges) confère la même orientation au périmètre extérieur (flèches bleues extérieures), recréant la situation de 1b (remarquez que les flèches bleues situées à côté de chaque arrête intérieure pointent en direction opposée et sont donc annulées). De nouveau, les points initial et terminal du périmètre coïncident et s’annulent à 0 où qu’ils se trouvent. Lorsque les segments périphériques adjacents sont identifiés comme indiqué par les flèches extérieures, le triangle se plie en un tétraèdre (2b). Ses faces forment un bord 2-dimensionnel fermé séparant son intérieur 3-dimensionnel de son extérieur, tandis que ses arrêtes forment un bord fermé 1-dimensionnel séparant ses faces les unes des autres. Mais maintenant, les flèches bleues s’annulent à chaque arrête et le bord 1-dimensionnel du bord 2-dimensionnel du tétraèdre est 0. Ainsi, pour le disque 2D et le tétraèdre 3D, le bord du bord est 0. Bien que les physiciens utilisent souvent cette règle pour expliquer la conservation de l’énergie-moment (ou comme l’appelle Wheeler, « momenergy » 20), elle peut être interprétée plus généralement en termes d’information et de contrainte, ou d’état et de syntaxe. En d’autres termes, le bord est analogue à une contrainte qui sépare un attribut intérieur satisfaisant la contrainte d’un attribut extérieur complémentaire, créant ainsi une distinction informationnelle.

Pas de question ? Pas de réponse ! Dans une expérience quantique, le dispositif de mesure et son emplacement correspondent à une question et le résultat à sa réponse. L’existence de la réponse, constituée d’informations sur l’état, est fondée sur le fait de poser la question (ou de l’occurrence de la mesure), et le type de réponse reçue dépend du type de question posée et de la manière dont elle est posée. Le monde est donc composé d’événements de mesure dans lesquels des informations sont échangées par des objets, l’un ou les deux « posant une question » et l’un ou les deux « donnant une réponse ». La question et la réponse, la stimulation et l’observation d’un événement, ne peuvent être séparées sur le plan ontologique et elles ne peuvent pas être protégées de l’influence de l’environnement. À la racine de ce critère sont l’incertitude quantique et la complémentarité, pierres fondatrices de la mécanique quantique.

Le Principe Super-Copernicien : De même que Copernic a remplacé le géocentrisme par l’héliocentrisme, montrant par extension qu’aucun lieu particulier dans l’univers n’est spécial et répudiant ainsi le « centrage-ici », le Principe Super-Copernicien dit qu’aucun moment particulier dans le temps n’est spécial, répudiant le « centrage-maintenant ». Essentiellement, cela signifie que lorsque l’observateur-participation fonctionne rétroactivement, la charge de la participation est effectivement distribuée dans le temps. Ainsi, bien que la « taille en bits » de l’univers soit trop importante pour avoir été entièrement générée par les observateurs-participants qui ont existé jusqu’à présent, les générations futures d’observateurs-participants, représentant éventuellement des modes d’observation-participation autres que celle associé à l’observation humaine, ont pesé et pèsent maintenant depuis l’avenir. (La pertinence de ce principe par rapport au Principe Anthropique Participatif va de soi.)

« La Conscience » : Wheeler souligne la difficulté d’établir une distinction générale entre la forme de traitement de l’information caractéristique des humains, et cette caractéristique de divers systèmes et dispositifs complexes qui peuvent ou non être « conscience ». « La ligne entre l’inconscient et le conscient commence à s’estomper… », déclare-t-il; « Nous devrons peut-être un jour élargir la portée de ce que nous entendons par un « qui ». » Le terme qui, suggère-t-il, est trop spécifique à l’homme, à la vie et à la conscience; ses connotations anthropiques sont anticoperniciennes, tandis que les concepts de vie et de conscience sont sujets à révision à mesure que la science avance. « Il semblerait plus raisonnable, » suggère-t-il, « de rejeter pour le moment les accents sémantiques de « qui », d’explorer et d’exploiter les connaissances à tirer des expressions « communication » et « communication employée pour établir un sens ». »21

Plus est différent : le potentiel de complexité augmente avec la cardinalité; avec un grand nombre d’éléments vient la variété combinatoire et le potentiel d’une sorte de structure logique à plusieurs niveaux qui caractérise les organismes biologiques et les ordinateurs modernes. C’est un précepte fondamental de la théorie de la complexité. Wheeler pose la question suivante : « Allons-nous un jour comprendre le temps et l’espace ainsi que toutes les autres caractéristiques qui distinguent la physique – et l’existence elle-même – en tant qu’organes auto-générés d’un système d’information auto-synthétisé ? » 22

Ensemble, ces slogans rigides, questions, précautions et indices constituent un appel à une nouvelle souche de théorie de la réalité, un modèle conceptuel unifié pour nos pensées et observations. Combien de modèles actuellement retenus répondent à cet appel ? La réponse est, bien sûr, « presque aucun ». Si certains d’entre eux semblent répondre à une ou deux des questions et respecter un ou deux des critères, aucune n’est toutefois proche de tous les aborder. Ce que chaque modèle a été obligé de donner pour répondre à un sous-ensemble de critères a coûté cher en termes de respect des autres. Nous avons donc une thèse et une antithèse sous forme de physique classique et de modèles quantiques discrets, mais parce que toute la profondeur de la relation entre les deux est insondable, aucune synthèse. Presque tout le monde semble reconnaître la justesse des idées de Wheeler, mais les relations hiérarchiques supérieures requises pour rassembler toutes ces informations dans une vision d’ensemble se sont révélées insaisissables. La difficulté logique de répondre à toutes les questions et de satisfaire tous les critères en même temps, en parallèle, à l’aide de concepts intégrés logiquement traitables, était tout simplement prohibitive.

Cette situation peut-elle être redressée ?

Quelques principes supplémentaires

Bien que les idées concernant la base idéale et/ou perceptuelle de la réalité remontent à des millénaires, nous pourrions tout aussi bien commencer par certains de leurs partisans les plus récents dans un souci de continuité. Premièrement, Descartes a postulé que la réalité est mentale au sens du rationalisme, mais a contredit sa propre thèse en introduisant le dualisme esprit-corps, la notion que l’esprit et la matière sont irréductiblement séparés. L’empiriste Berkeley a alors déclaré que la réalité était de nature perceptuelle, une sorte de croisement entre l’esprit et la matière. On peut le voir en soustrayant mentalement la perception de la conception de la réalité; ce qui reste est de la pure cognition subjective, mais sans aucun grain objectif pour le moulin perceptuel. (Bien que les tentatives de soustraction cognitive de la réalité sur le plan cognitif soient bien plus courantes, elles ressemblent un peu à vouloir montrer qu’une éponge n’est pas mouillée de manière inhérente lorsqu’elle est immergée dans l’eau, elles ne peuvent jamais réussir sur les parties d’entités cognitives.) Hume a ensuite tenté de supprimer complètement la cognition et la causalité, affirmant que l’esprit et la matière sont tous deux inhérents à la perception et n’existent ni en dehors ni l’une sans l’autre.

En se débarrassant de l’esprit, Hume a apporté une autre « contribution » importante à la théorie de la réalité : il a tenté de se débarrasser de la causalité en la considérant comme un artefact cognitif, en appuyant sa thèse sur le problème de l’induction.23 Le problème de l’induction énonce que, comme l’induction empirique implique l’hypothèse préalable de ce qu’elle cherche à établir, à savoir l’uniformité de la nature, la science est circulaire et fondamentalement défectueuse. Le problème de l’induction est tout à fait réel; cela se manifeste dans l’incertitude d’Heisenberg et le problème de l’horizon cosmique, les limites finies des outils scientifiques d’observation microscopique et macroscopique, et explique pourquoi aucune théorie générale de la réalité ne peut jamais être construite de manière fiable par les méthodes empiriques classiques de la science. Malheureusement, de nombreux scientifiques ont soit écarté ce problème, soit abandonné discrètement la recherche d’une théorie véritablement générale, ne servant aucunement les intérêts à long terme de la science. En fait, le problème de l’induction implique simplement qu’une théorie globale de la réalité ne peut être établie que par les méthodes rationnelles des mathématiques, y compris spécifiquement celles de la logique.

En réponse à Berkeley et Hume, Kant a affirmé que la connaissance non traitée qui subsiste lorsque le contenu perceptuel est soustrait possède une structure intrinsèque qui existe avant le contenu; elle comprend les catégories a priori de réalité perceptuelle ou « phénoménale ».24 Malheureusement, soustraire la perception selon les règles kantiennes donne plus que des cognitions non traitées; cela donne aussi des noumènes, des objets absolus ou des « choses en elles-mêmes ». D’un côté du résultat, il y a un isomorphisme perceptuel entre l’esprit et la réalité phénoménale; de l’autre côté, il y a un gouffre au-delà duquel se trouve une réalité nouménale inconnaissable mais néanmoins fondamentale, que Kant considérait évidemment comme le dernier mot de la théorie de la réalité (sous-théologique).

Cependant, l’abîme de Kant est si profond et si large, et interdit si soigneusement tout isomorphisme esprit-réalité, qu’il exclut l’efficacité causale et, par là même, tout autre principe de correspondance compréhensible. Cela implique que les noumènes sont à la fois rationnellement et empiriquement non pertinents pour la réalité cognitive et perceptuelle et qu’ils peuvent donc être éliminés de la théorie de la réalité en toute sécurité. Quel que soit ce que Kant avait à l’esprit quand il a introduit le concept de noumène, sa définition revient essentiellement à un « concept inconcevable » et est donc un oxymore. Quoi qu’il ait réellement voulu dire, nous devons nous fier à autre chose que la métaphysique kantienne pour le trouver. 25

Jusqu’ici, nous avons réussi à réduire la réalité à la réalité phénoménale étudiée par la science, une combinaison de contenu perceptuel et de principes rationnels de cognition. Un scientifique utilise des méthodes empiriques pour effectuer des observations spécifiques, applique les relations cognitives générales issues de la logique et des mathématiques afin de les expliquer, et parvient à traiter la réalité comme un mélange de perception et de cognition. Mais ce traitement manque de quelque chose qui ressemble à une justification explicite. Lorsqu’une série d’observations est expliquée avec une série probable d’équations interprétées, l’adhérence entre l’explicandum et l’explication pourrait tout aussi bien être fournie par un ciment en caoutchouc. C’est-à-dire que les explications et les interprétations scientifiques font coller les observations et les équations d’une manière très mal comprise. Cela fonctionne souvent comme un charme… mais pourquoi ? L’un des principaux objectifs de la théorie de la réalité est de répondre à cette question.

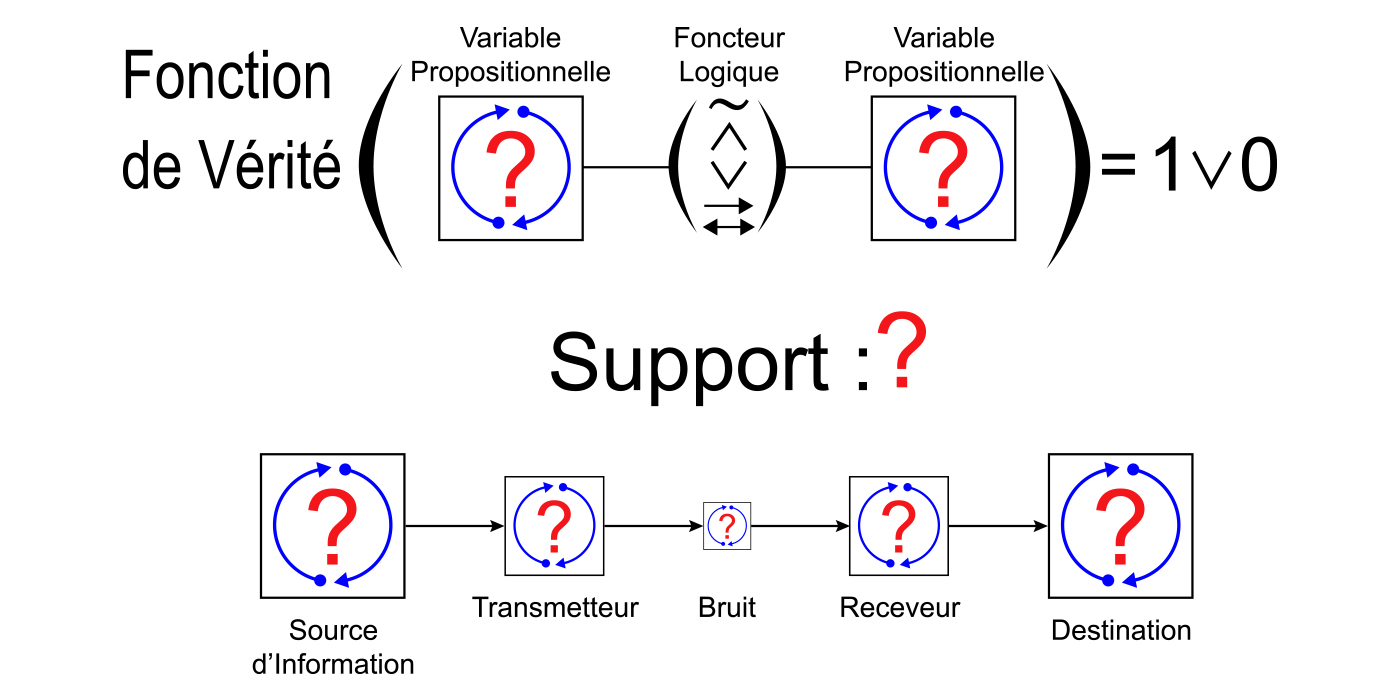
La première chose à noter à propos de cette question est qu’elle implique le processus d’attribution et que les règles d’attribution sont définies en étapes par une logique mathématique. La première étape est appelée logique propositionnelle et contient les règles d’attribution des attributs vrai ou faux, désignant respectivement l’inclusion ou la non-inclusion dans des systèmes cognitifs-perceptuels arbitraires, à des relations hypothétiques dans lesquelles des prédicats sont liés par les foncteurs logiques non, et, ou, implique, et si et seulement si. La logique propositionnelle définit ces foncteurs comme des fonctions de vérité attribuant des valeurs de vérité à de telles expressions indépendamment du contenu (mais pas des valeurs de vérité) de leurs prédicats, créant ainsi une définition circulaire des foncteurs sur les valeurs de vérité et des valeurs de vérité sur les foncteurs. L’étape suivante de l’attribution, la logique des prédicats, attribue des propriétés spécifiques aux objets à l’aide de quantificateurs. Et l’étape finale, la théorie des modèles, comprend les règles permettant d’attribuer des relations complexes de prédicats à des relations complexes d’objets, c’est-à-dire des théories à des univers. De plus, la forme d’attribution appelée définition est expliquée dans une branche logique centrée sur la théorie appelée théorie formalisée, et la mécanique de l’attribution fonctionnelle est traitée dans la théorie de la récursion.

En logique propositionnelle, une tautologie est une expression de variables propositionnelles liées à un foncteur qui est toujours vraie, quelles que soient les valeurs de vérité attribuées à ses variables propositionnelles elles-mêmes. Une tautologie a trois propriétés clés: elle est universellement (syntactiquement) vraie, elle est donc autoréférentielle (vraie même d’elle-même et donc fermée dans une auto-composition récursive) et ses implications restent consistantes dans des opérations inférentielles préservant ces propriétés. C’est-à-dire que chaque tautologie est une circularité auto-consistante de portée universelle, possédant la validité en vertu de la fermeture dans une auto-composition, l’exhaustivité (non-exclusion de la vérité) et la consistance (l’absence de paradoxe insoluble). Mais les tautologies ne sont pas simplement cohérentes en elles-mêmes; elles sont mutuellement consistantes dans une composition mutuelle, faisant de la logique propositionnelle autant une « circularité auto-consistante de portée universelle » que n’importe laquelle de ses tautologies. Ainsi, la logique propositionnelle comprend deux niveaux de tautologie, l’un s’appliquant aux expressions et l’autre aux systèmes théoriques. La logique des prédicats étend ensuite le concept de tautologie aux actes d’attribution spécifiques représentés par les variables propositionnelles (auparavant anonymes), et la théorie des modèles englobe ensuite des actes d’attribution plus complexes impliquant des relations plus complexes.

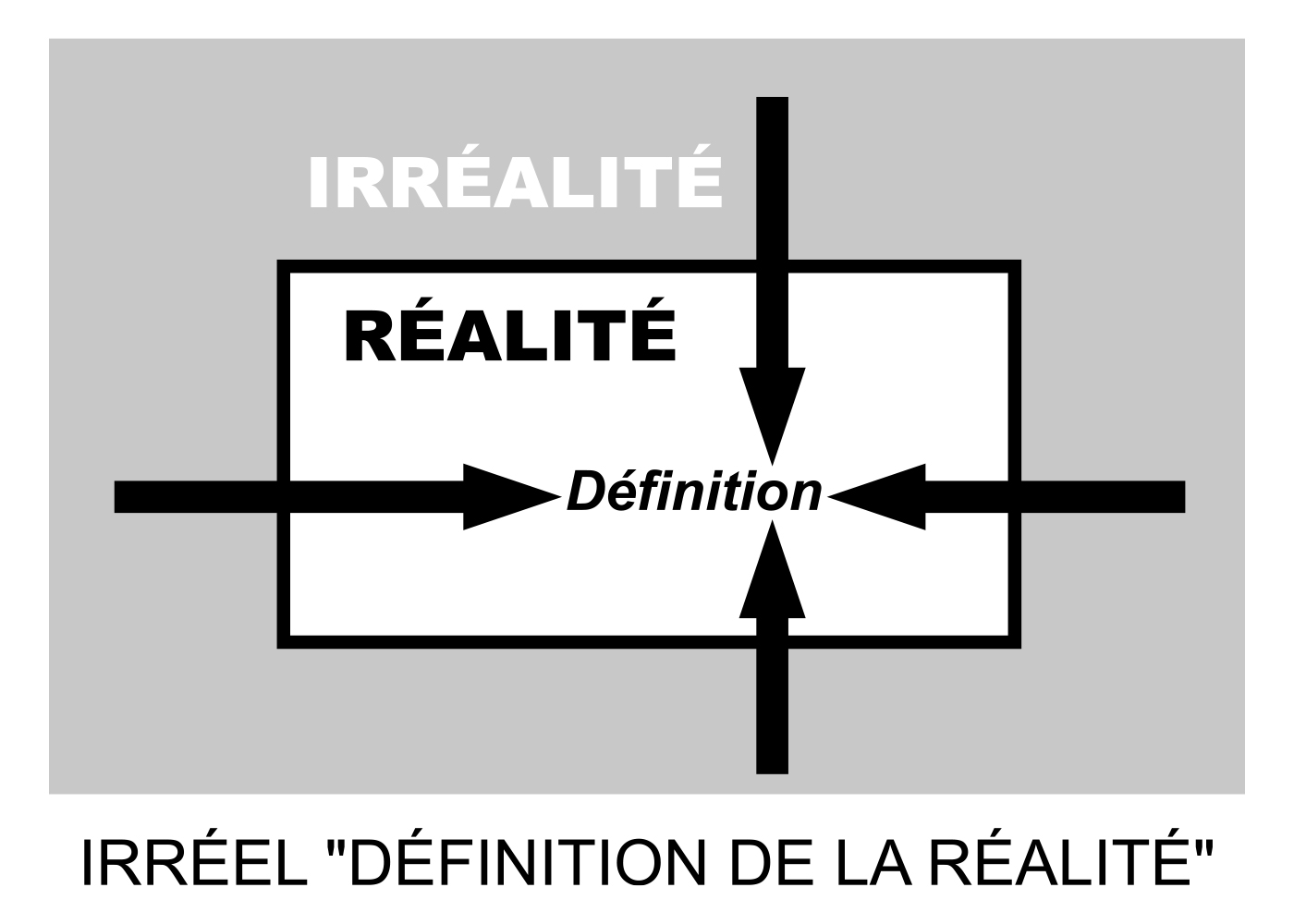
La théorie de la réalité concerne l’étape d’attribution dans laquelle deux prédicats analogues au vrai et au faux, à savoir le réel et l’irréel, sont attribués à diverses déclarations sur l’univers réel. En ce sens, il est étroitement lié à la logique propositionnelle. En particulier, la logique propositionnelle a quatre propriétés principales à émuler par la théorie de la réalité. La première est la vérité absolue; en tant que définition formelle de la vérité, elle est vraie par définition. Les autres propriétés sont la fermeture, l’exhaustivité et la consistance. C’est-à-dire que la logique est entièrement basée sur, et définie strictement dans les limites, de la cognition et de la perception; elle s’applique à tout ce qui peut être perçu ou conçu de manière cohérente; et elle est par nature consistante, étant conçue de manière à exclure toute inconsistance. C’est la base des mathématiques, le moyen par lequel les propositions sont énoncées, prouvées ou réfutées, et c’est le cœur de la science, garantissant l’intégrité de la méthodologie rationnelle et empirique. Même les logiques dites « non standard », par exemple les logiques modales, floues et à valeurs multiples, doivent être exprimées en termes de logique fondamentale à deux valeurs pour avoir un sens. En bref, la logique à deux valeurs est quelque chose sans laquelle la réalité ne pourrait pas exister. Si elle était éliminée, alors vrai et faux, réel et irréel, et existence et non-existence ne pourraient pas être distingués, et le moindre acte de perception ou de cognition serait tout à fait impossible.

Jusqu’ici, il a été largement admis que la théorie de la réalité peut être recherchée par les mêmes moyens que toute autre théorie scientifique. Mais ce n’est pas tout à fait vrai, car si la science utilise l’équivalent épistémologique de la colle magique pour lier ses théories à ses observations, la théorie de la réalité doit en donner une recette et en justifier les moyens d’application. En d’autres termes, la théorie de la réalité doit décrire la réalité à un niveau qui justifie la science et donc occuper un niveau d’explication plus profond que la science elle-même. Cela signifie-t-il que la théorie de la réalité est mathématique ? Oui, mais puisque les mathématiques doivent être justifiées avec la science, métamathématique serait peut-être une meilleure description… et quand tout est dit et fait, cela revient à la logique pure et simple. Il s’ensuit que la théorie de la réalité doit prendre la forme d’une logique étendue… en fait, une « forme limitante » de la logique dans laquelle la relation entre théorie et univers, jusqu’ici source inépuisable d’ambiguïté modèle-théorique destructrice, est enfin réduite à une forme monique (d’aspect double), court-circuitant le paradoxe du dualisme cartésien et éliminant le fossé épistémologique entre esprit et matière, théorie et univers.

À mesure que la complexité augmente et que les prédicats deviennent des théories, tautologie et vérité deviennent plus difficiles à reconnaître. Parce qu’universalité et spécificité sont contraires dans la pratique sinon en principe, elles sont soumises à une sorte de « décohérence logique » associée à une stratification relationnelle. Comme les prédicats ne sont pas toujours tautologiques, ils sont sujets à divers types d’ambiguïtés; à mesure qu’ils deviennent de plus en plus spécifiques et complexes, il devient de plus en plus difficile de contrôler localement l’héritabilité de la consistante et de conserver localement la propriété de vérité au cours de l’attribution (ou même après coup). Indécidabilité26, insolubilité LSAT et NP-complétude, ambiguïté des prédicats et théorème de Lowenheim-Skolem, ambiguïté observationnelle et thèse de Duhem-Quine27… sont quelques-uns des problèmes qui apparaissent une fois que le prédicat de vérité « décohére » par rapport aux modélisations attributives complexes. C’est pour de telles raisons que la philosophie de la science s’est rabattue sur la doctrine falsificationniste, renonçant à la base tautologique de la logique, transformant effectivement la vérité en statut provisoire et décourageant une pleine appréciation du niveau tautologique-syntactique de la recherche scientifique, et même de la logique et de la philosophie elles-mêmes.

En fait, la validité des théories scientifiques et de la science dans son ensemble dépend absolument de l’existence d’un cadre réalité-théorique fondamental couvrant l’ensemble de la science… une syntaxe fondamentale à partir de laquelle tous les langages scientifiques et mathématiques, et le langage cognitif étendu de la perception elle-même, peut être déplié grammaticalement, croisé et validé. La tautologie, base théorique de la vérité telle qu’elle est incarnée dans la logique propositionnelle, est évidemment au cœur de cette syntaxe. En conséquence, la théorie de la réalité doit être développée par l’amplification de cette syntaxe tautologique par adjonction de composants syntactiques supplémentaires, les principes de la théorie de la réalité, qui laissent le caractère général de la syntaxe invariant. Plus précisément, pour élaborer une théorie de la réalité qui ait la propriété de vérité au même sens que la logique la possède, mais permette l’évaluation logique des déclarations concernant l’espace, le temps et les lois, nous devons jouxter des principes d’extension qui donnent un sens à de telles déclarations tout en préservant la propriété de tautologie.

Selon la nature de la logique propositionnelle, la vérité est tautologiquement basée sur l’intégrité de la réalité cognitive et perceptuelle. La cognition et la perception comprennent la base primitive (auto-définitive) de la logique, et la logique comprend les règles de structure et d’inférence en vertu desquelles la perception et la cognition sont stables et cohérentes. Donc, lorsque nous disons que la vérité est héritable en vertu de règles logiques d’inférence, nous entendons en réalité que la tautologie est héritable et que la base cognitive-perceptuelle primitive de la logique propositionnelle conserve ainsi son statut principal. En convertissant les tautologies en d’autres tautologies, les règles d’inférence de la logique propositionnelle convertissent les invariants cognitifs-perceptuels en d’autres invariants. Pour poursuivre ce programme dans la théorie de la réalité, nous devons identifier des principes décrivant comment la structure en boucle de la tautologie logique est manifeste dans divers configurations et contextes réalité-théoriques à différents niveaux de description et d’interprétation; de cette façon, nous pouvons vérifier sa conservation dans les opérations de réduction et d’extension théoriques. C’est-à-dire que nous devons jouxter les principes généralisés de la structure bouclée à la syntaxe logique de manière à ce que de plus en plus de la réalité soit ainsi expliquée et que l’exhaustivité soit réalisée.

Par exemple, prenons la tautologie propositionnelle « X v ~ X » (X OU NON-X). Appliqué à la perception, cela signifie que lorsque quelque chose est vu ou observé, il n’est pas vu en conjonction avec son absence; si c’était le cas, alors deux perceptions contradictoires coïncideraient, aboutissant à un « éclatement » des réalités perceptuelles. En effet, soit la conscience de celui qui perçoit serait scindée en deux réalités cognitives distinctes dans un cas de dissociation en chaîne réactive, soit le spectateur lui-même se scinderait physiquement avec la réalité physique. Quand « X v ~ X » est composé avec d’autres tautologies (ou lui-même) par substitution, les enjeux sont exactement les mêmes; toute violation de la tautologie composée diviserait la réalité perceptuelle et cognitive avec des implications désastreuses pour son intégrité.28

Après sa nature tautologique, la première chose à noter à propos de la logique propositionnelle dans le contexte de la théorie de la réalité est que, contrairement à l’esprit dans lequel elle a été fondée – elle représente, après tout, les règles des processus mentaux29 de la cognition qui semble lui conférer un caractère mental dès le début – elle présente une insuffisance fonctionnelle fondamentale : elle semble nécessiter un logicien externe pour le lire, le comprendre et l’appliquer mentalement. D’autre part, la nature (ou la réalité cognitive-perceptuelle) ne nécessite aucun logicien externe pour appliquer les règles de la logique. Par conséquent, les principes tautologie-préservant proposés de la théorie de la réalité devraient replacer l’esprit dans le mélange de manière explicite et théoriquement traitable, en dotant la logique de « capacité de traitement automatique ». Après tout, c’est exactement ce qu’elle possède dans sa manifestation naturelle, la réalité au sens large, et une dimension essentielle de la propriété de fermeture sans laquelle la vérité est insoutenable. C’est-à-dire que la réalité doit pouvoir se reconnaître et conférer cette capacité à ses composants en tant que condition de leur existence et de leurs interactions.

Après avoir expliqué les principaux problèmes techniques de la théorie de la réalité, nous pouvons passer maintenant à la chasse : la façon de construire une théorie de la réalité consiste à identifier les propriétés qu’elle doit inconditionnellement posséder pour exister, mettre au point la théorie en la définissant comme possédant ces propriétés sans introduire simplement des propriétés contingentes qui, si elles étaient considérées comme générales, pourraient nuire à leur relation descriptive avec l’univers réel (celles-ci peuvent venir plus tard et seront naturellement sujettes à une confirmation empirique). En d’autres termes, les moyens utilisés pour construire la théorie doivent être rationnels et tautologiques, tandis que ceux permettant de l’affiner ultérieurement peuvent être empiriques. Puisque nous voulons que notre théorie soit suffisamment inclusive, suffisamment exclusive et suffisamment consistante pour faire le boulot de décrire la réalité, ces propriétés incluront certainement l’exhaustivité (moins complète mais aussi moins indécidable que la complétude), la fermeture et la consistance. À ces propriétés, les « 3 C » [NDT : Comprehensiveness, Closure, Consistency], nous allons assigner trois principes de forme essentiellement tautologique; De cette manière, les relier à la théorie de la réalité basée sur la logique préservera la propriété de tautologie de la logique, excluant rationnellement l’incertitude par les mêmes moyens que la logique elle-même. Une théorie de la réalité construite de cette manière est appelée supertautologie.

Parce que nos trois principes correspondent aux 3 C et qu’ils commencent tous par la lettre M, nous pourrions aussi bien les appeler les « 3 M » : M = R, MAP et MU, respectivement pour le Principe Mind Equals Reality, le Principe de l’Autologie Métaphysique et le Principe de d’Unité Multiplexe. Le principe M = R, propriété théorique tautologique qui dissout la distinction entre théorie et univers et identifie ainsi l’univers réel comme une « théorie auto-réifiante », rend la syntaxe de cette théorie exhaustive en veillant à ce que rien qui puisse être cognitivement ou perceptiblement reconnu comme faisant partie de la réalité ne soit exclu faute de syntaxe. MAP rend tautologiquement cette syntaxe fermée ou autonome dans les sens définitif, descriptif et interprétatif et, conjointement avec M = R, rend l’univers parfaitement autonome dans l’affaire. Et MU rend tautologiquement cette syntaxe, et le complexe théorie-univers qu’elle décrit, suffisamment cohérente pour assurer sa propre consistance (ainsi, le « C » correspondant à MU se divise en fait en deux C, consistance et cohérence, nous en avons donc quatre en tout). Pour chacun de ces principes nous pouvons ajouter toutes corollaires utiles qui se présentent.30

Comme il est du domaine de tout théoricien de la réalité d’utiliser des propriétés de la réalité pour expliquer la réalité et que ces propriétés sont définies de manière récursive, nous ferons parfois référence implicitement ou explicitement à diverses propriétés dans les descriptions d’autres propriétés. Cela exclut une série habile de définitions cumulatives, ce qui n’est possible dans tous les cas qu’en prenant pour acquis le contenu et les moyens de la théorisation (on ne peut malheureusement rien prendre pour acquis dans la théorie de la réalité). Comme nous le verrons plus loin, la nature récursive de la CTMU est inévitable. Deuxièmement, le CTMU est développé « à l’envers » par rapport aux théories déductives habituelles de la science et des mathématiques, en éliminant d’abord les contraintes et en utilisant ensuite seulement les résultats pour déduire des faits à propos du contenu. La plupart des théories commencent par des axiomes, des hypothèses et des règles d’inférence, extraient des implications, testent logiquement ou empiriquement ces implications, puis ajoutent ou révisent les axiomes, les théorèmes ou les hypothèses. Le CTMU fait l’inverse, éliminant les suppositions et « reconstruisant la réalité » tout en ne rajoutant aucunes suppositions.

Les principes suivants sont présentés en trois étapes. La première étape inclut le Principe de Réalité, le Principe de Réductibilité Linguistique et le Principe de Syndifféonèse, qui peuvent être considérés comme préliminaires à MAP, M = R et MU respectivement (l’ordre de présentation peut différer légèrement de celui qui vient d’être donné). La deuxième étape comprend MAP, M = R et MU eux-mêmes, tandis que la troisième étape consiste en plusieurs principes auxiliaires pouvant être considérés comme leurs conséquences.

Le Principe de Réalité

La réalité, c’est-à-dire l’univers réel, contient tout et seulement ce qui est réel. Le concept de réalité est analytiquement autonome; s’il y avait quelque chose hors de la réalité qui était suffisamment réel pour affecter ou influencer la réalité, il serait à l’intérieur de la réalité, et cette contradiction invalide toute supposition d’une réalité externe (jusqu’à la pertinence d’observation ou théorique).31

Bien que cette caractérisation de la réalité incorpore une définition circulaire de la pertinence, la circularité est essentielle au concept de réalité et n’exclut pas une base perceptuelle (observationnelle, scientifique). En effet, nous pouvons affiner la définition de la réalité comme suit : « La réalité est l’agrégat perceptuel comprenant (1) toutes les observations scientifiques qui ont été et seront faîtes, et (2) l’entière infrastructure explicative abstraite et/ou cognitive de la perception » (où l’abstrait est une généralisation syntactique de la signification concrète d’idées, de concepts ou de structures cognitives distribuées sur des instances physiques qui s’y conforment en tant que contenu conforme à la syntaxe).

Diagramme 5

Il convient de noter que toute définition revient à une théorie microscopique de la chose définie. Le Principe de Réalité, qui peut être considéré comme une définition générale de la réalité, en est un exemple; cela peut être considéré comme le germe d’une théorie de la réalité que nous avons maintenant commencé à construire. En définissant la réalité comme autonome, cette « microthèorie » se dote d’une forme simple de fermeture ; elle ne fait appel à rien en dehors du definiendum au cours de sa définition, et interdit effectivement à toute extension future de cette définition de le faire (ceci devient explicite dans un principe connexe, le MAP).

Mais revenons maintenant à la liste. Jusqu’ici, nous avons appris que la réalité est autonome; elle est partout la même chose qu’elle-même. Qu’en est-il de toutes ses distinctions internes ?

La Syndifféonèse

La réalité est une relation, et chaque relation est une relation syndifféonique présentant une syndifféonèse ou « différence dans la similitude ». La réalité est donc une relation syndifféonique. La syndifféonèse implique que toute affirmation selon laquelle deux choses sont différentes implique qu’elles sont par réduction les mêmes; si leur différence est réelle, elles se réduisent toutes les deux à une réalité commune et sont dans cette mesure similaires. La syndifféonèse, le plus général des principes réducteurs, forme la base d’une nouvelle vision de la structure relationnelle de la réalité.

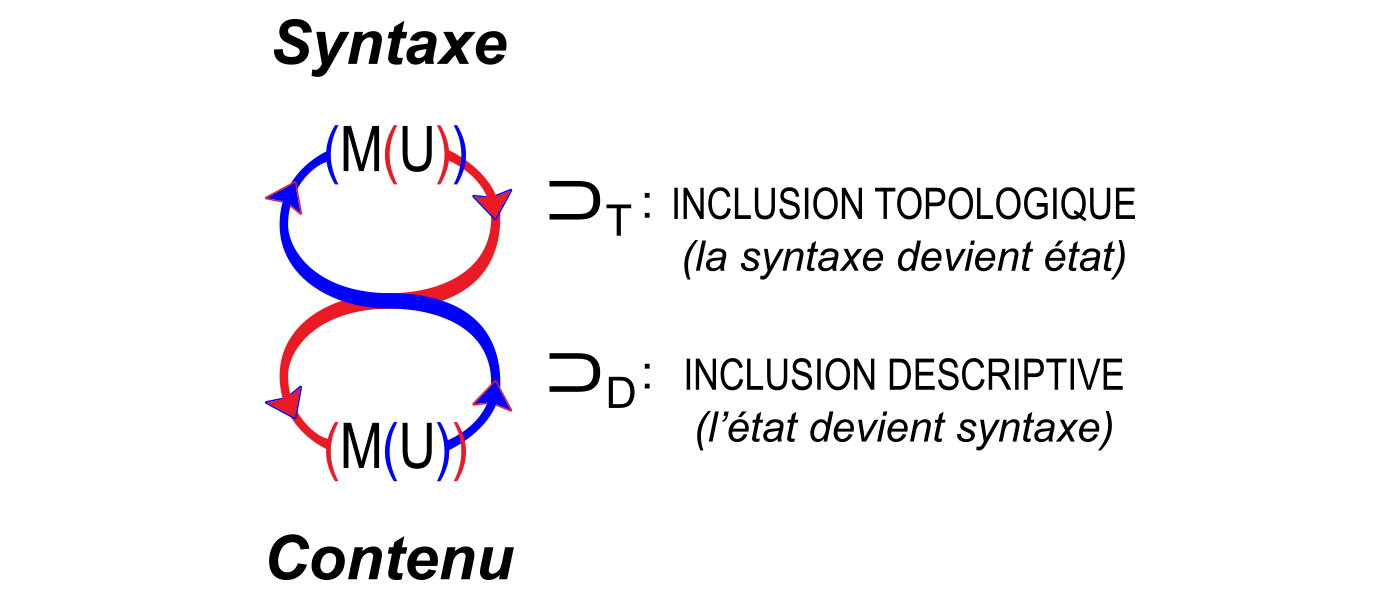
Le concept de syndifféonèse peut être saisit en affirmant que l’expression et/ou l’existence de toute relation de différence comprend un support et une syntaxe communs, c’est-à-dire les règles d’état et de transformation caractérisant le support. C’est de ces règles que la relation tire ses caractéristiques spatiales et temporelles telles qu’exprimées à l’intérieur du support. Ainsi, une relation syndifféonique consiste en une relation de différence intégrée dans un support relationnel dont les règles distribuées de structure et d’évolution soutiennent son existence.

Chaque relation syndifféonique a des phases synétiques et difféoniques présentant respectivement une synèse et une difféonèse (similitude et différence, ou distributivité et localité paramétrique), et présente deux formes de confinement, topologique et descriptif. Le support est associé à la phase synétique, tandis que la relation de différence est associée à la phase difféonique (les règles d’état et la transformation du support y étant distribuées, le support est homogène, ne possédant intrinsèquement qu’une extension relative du fait des relations de différence qu’il contient). Les retours difféoniques étant liés à leur support d’expression commun et à sa syntaxe distributive de manière à combiner les aspects d’union et d’intersection, l’opération produisant le support à partir des retours s’appelle unisection (U). Le support synétique représente le potentiel difféonique dont la relation de différence est une actualisation.

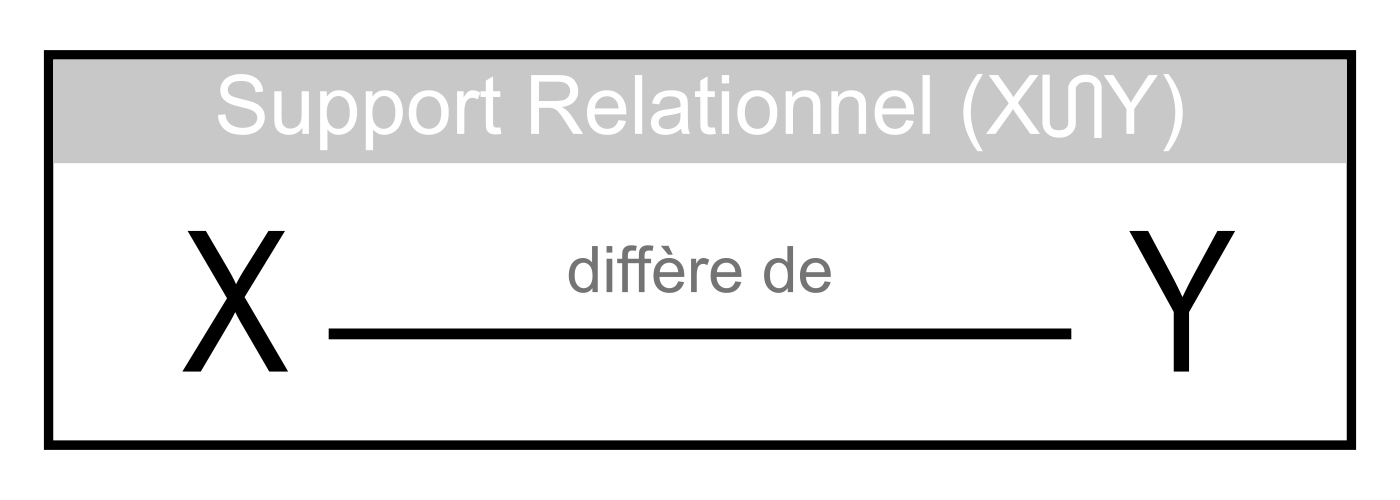
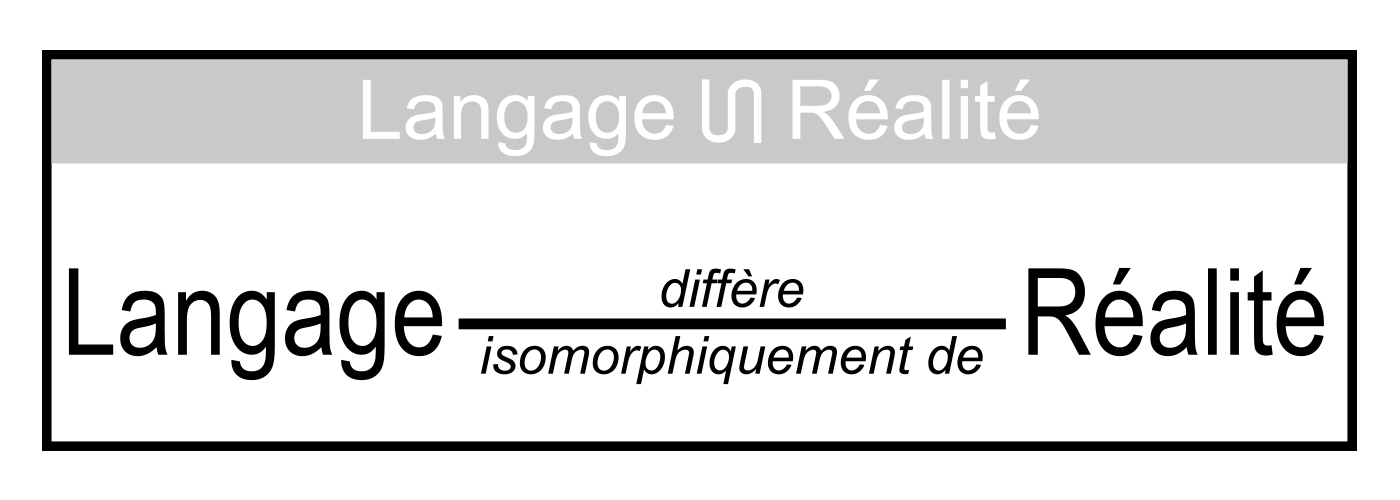
Diagramme 6 : Ce diagramme syndifféonique générique illustre un fait simple : toute relation de différence nécessite un support avec extension dans le paramètre différentiel. Comme illustré, le support distribue à la fois la relation linéaire « X diffère de Y » et de ses retours (entités liées) X et Y, leur conférant une propriété « de parenté » commune équivalant à « l’inclusion dans le support relationnel XUY », où XUY est le produit unisecte ou « produit syntactique » de X et Y. Cet attribut commun invalide toute affirmation selon laquelle la différence entre les retours est « absolue » ou « irréductible »; le simple fait que la différence puisse être exprimée linguistiquement ou géométriquement implique qu’elle n’est que partielle et que les deux retours sont des manifestations d’un seul et même support ontologique. Lorsque X et Y représentent des parties ou des aspects arbitraires de la relation de différence appelée réalité, ce diagramme montre graphiquement que la réalité consiste finalement en un support ontologique unitaire. En conséquence, la théorie de la réalité doit être une théorie monique réduisant la réalité à ce support (cette idée est développée plus avant dans le Principe du Monisme Infocognitif).

Notez que toute inhomogénéité syntactique (par opposition à informationnelle) dans le support commun est en soi une relation de différence et invite donc à une reconstitution du diagramme. De même, toute inhomogénéité dans le support commun illustrée par le diagramme recréé inviterait une autre reproduction du diagramme, etc. Toute régression syndifféonique de ce type doit prendre fin, car sinon, il n’y aurait pas de syntaxe stable et donc pas de « relation » suffisamment stable pour être perçue ou conçue. La stabilité informationnelle de la réalité perceptuelle montre que la syntaxe de la réalité est stable.

Le diagramme ci-dessus pourrait être exprimé de manière compacte comme suit: syn(XUY):diff(X, Y). Par exemple, syn(nomAX U nomBX):diff(nomAX, nomBX) signifie que lorsque nomAX, nomBX sont des ensembles de lois auxquelles le système X obéit à différents moments, emplacements ou cadres de référence A et B dans le système X, il existe un ensemble plus fondamental de lois (nomAX U nomBX) en fonction duquel cette différence peut être exprimée. Cela montre qu’à un certain niveau, la covariance générale doit tenir. Ce n’est pas simplement vrai « jusqu’à l’isomorphisme avec X »; même si plusieurs ensembles de lois valides peuvent être distingués, l’un d’entre eux pouvant être actif à un endroit donné (A, B,…) dans X [XA ⊨nom1, XB ⊨nom2, …, où les indices numériques désignent la distinction nomologique], toute différence distinguable entre ces ensembles nécessite également une syntaxe commune. La cohérence informationnelle est donc une condition sine qua non d’une existence reconnaissable; tout système dans lequel elle échouerait se décohérerait simplement faute de quoi tenir.

En d’autres termes, (1) lorsque des distinctions d’information concernant un système X sont considérées comme des instanciations de loi, elles peuvent également être considérées comme des expressions conformes à la syntaxe; et (2) l’expression des différences nécessite une syntaxe d’expression unifiée (ou ensemble de « lois »), et cette syntaxe doit être distribuée sur l’ensemble des expressions différentielles (ou « instanciations de loi »). Par exemple, lorsque X est une « intersection perceptuelle » constituée d’objets, d’attributs et d’événements généralement reconnaissables, les lois de la perception doivent en définitive être constantes et distribuées. Lorsqu’il existe une différence nomologique présumée pour une paire de loci (A, B), la covariance syntaxique réductive s’applique en raison de la nécessité d’un support d’expression et, lorsqu’il n’existe de telle différence pour n’importe quelle paire de loci (A, B), la covariance syntactique s’applique a fortiori sans besoin de réduction.

Les relations syndifféoniques peuvent être considérées comme des éléments de réseaux infocognitifs plus complexes ayant des dimensions spatiales et temporelles (ordinales, stratificatives). Interprétés selon les principes de dualité du CTMU, les réseaux infocognitifs comprennent des relations logiques d’état et de syntaxe. La régression d’un de ces réseaux par unisection conduit finalement à un support syntaxique d’une généralité et d’une homogénéité parfaite… un « opérateur syntactique » universel et réflexif.

En effet, la syndifféonèse est en effet une tautologie métalogique équivalant à un paradoxe d’auto-résolution. Le paradoxe réside dans la coïncidence de la similitude et de la différence, tandis qu’une résolution de type théorique est inhérente à la distinction logique et mathématique qui les sépare, c’est-à-dire à la dimension stratificative d’un réseau infocognitif.32 Ainsi, réduire la réalité à une syndifféonèse revient à la « paradoxiformer ». Cela a un avantage : une théorie et/ou une réalité construite d’un paradoxe auto-résolvant est immunisée contre le paradoxe.

Jusqu’ici, nous savons que la réalité est une relation syndifféonique autonome. Nous avons également accès à un type de diagramme instructif que nous pouvons utiliser pour illustrer certains des principes qui suivent. Voyons donc si nous pouvons en apprendre davantage sur le type de relation syndifféonique autonome qu’est la réalité.

Le Principe de la Réductibilité Linguistique

La réalité est une forme de langage autonome. Cela est vrai pour au moins deux raisons. Premièrement, bien qu’elle soit matérielle et concrète à certains égards, la réalité est conforme à la définition algébrique d’un langage. C’est-à-dire qu’elle intègre

(1) des représentations d’individus (analogues à des objets), des relations et attributs (analogues à l’espace) et des fonctions et opérations (analogues au temps);

(2) un ensemble d’« expressions » ou d’états perceptuels; et

(3) une syntaxe consistant en (a) des règles de structure logiques et géométriques, et (b) une grammaire générative inductive-déductive identifiable aux lois de la transition d’état.

Deuxièmement, comme la perception et la cognition sont des langages et que la réalité est de nature cognitive et perceptuelle, elle est également un langage.

Bien qu’il y ait eu beaucoup de programmes réductionnistes en science et en philosophie, la réduction promise est toujours la même : un langage théorique. Parce que c’est nécessairement vrai, le langage est fondamental. Le fait que la plupart de ces théories, par exemple les théories de la physique, soulignent le statut fondamental de quelque chose d’« objectif » et d’« indépendant du langage », par ex. la matière et/ou l’énergie, n’a aucune importance, car le fait d’indiquer lui-même invoque un isomorphisme entre la théorie et la réalité objective… un isomorphisme soumis au Principe de Réalité, et qui ne pourrait exister que si la réalité partageait la structure linguistique de la théorie elle-même.

Peut-être le sens de ce principe peut-il être exprimé de la manière la plus concise par une généralisation de l’aphorisme « Ce dont on ne peut pas parler, il faut le taire » : ce qui ne peut être décrit linguistiquement ne peut être ni perçu ni conçu. Ainsi, à des fins théoriques et observationnelles de la science et de la théorie de la réalité, ce qui est non isomorphe au langage est au-delà de toute considération en tant que composant de la réalité.

Diagramme 7 : Dans ce diagramme syndifféonique, l’affirmation « Le langage diffère de la réalité » est présentée le long d’un segment de droite prolongé représentant la différence supposée entre les retours. Tout comme dans le diagramme générique ci-dessus, les deux retours possèdent l’attribut « inclusion dans le support syntaxique relationnel (Langage U Réalité) ». Parce qu’ils sont tous deux des manifestations du même support sous-jacent, leur différence ne peut être absolue; à un niveau fondamental, la réalité et la langue partagent des aspects communs. Ceci est consistant avec la nature de la relation de « différence », qui est en réalité supposée représenter un isomorphisme sémantique et modèle-théorique.

Comme nous l’avons déjà vu, le Principe de Réalité dit que la réalité contient tout et seulement ce qui est réel. Tel que défini par cette affirmation, le prédicat réalité est principalement une construction linguistique conforme à la structure syntactique, où la syntaxe consiste en des règles selon lesquelles les prédicats sont construits et interprétés. En ce sens, la réalité constitue une sorte de théorie dont les axiomes et les règles d’inférence sont implicitement fournis par la composante logique de la syntaxe conceptuelle dans laquelle elle est exprimée. Le Principe de la Réductibilité Linguistique ne fait que clarifier la question de savoir si la réalité est un prédicat linguistique ou le contenu objectif d’un tel prédicat en affirmant qu’il s’agit des deux. Ainsi, lorsque le prédicat de réalité est analytiquement (ou syntactiquement) autonome, la réalité est autonome. Ceci peut être exprimé comme suit : au niveau de la syntaxe cognitive-perceptuelle, la réalité équivaut à la théorie de la réalité. Là où la théorie et l’univers convergent, le rasoir d’Occam et les principes physiques d’économie deviennent des tautologies.

Parce que la perception est une intersection sensorielle de l’esprit et de la réalité, la perception est impossible sans cognition, et dans cette mesure, le prédicat cognitif réalité équivaut à leur contenu perceptuel. Au niveau de la syntaxe cognitive et perceptuelle, le langage est nécessairement isomorphe à ce qu’il décrit; dans une réalité perceptuelle comme celle qui existe autour de nous, il est tautologiquement vrai que le langage de base de la cognition et de la perception est syntaxiquement isomorphe à la réalité (bien que l’illusion et le mensonge deviennent possibles au niveau sémantique). Il s’ensuit que nous pouvons parler de réalité en termes de cognition et perception généralisées, où cette phrase dénote la conformité à la cognition et à la perception au niveau syntaxique. En particulier, la cognition généralisée est ce processus par lequel la réalité « se reconnaît » partout.

Le Principe de la Réductibilité Linguistique donne le mandat d’ajouter une forme avancée de théorie du langage à l’arsenal mathématique de la théorie de la réalité. Les avantages réalité-théoriques de cet ajout sont incalculables. Dans la théorie physique conventionnelle, les entités fondamentales sont des particules ponctuelles, des ondes et plus récemment des cordes; chaque classe d’objet a ses problèmes et ses paradoxes. Dans le CTMU, les objets fondamentaux sont des opérateurs syntactiques (unités d’informations auto-transductives ou infocognition) capables non seulement d’émuler tous ces objets et plus, mais aussi de contenir les structures syntaxiques auxquelles ils doivent inévitablement se conformer et résoudre leurs paradoxes caractéristiques dans l’échange. Parce que le sens équivaut à la connectivité sémantique et est donc linguistique dans tous les sens du terme, le passage à une perspective linguistique est indispensable à la téléologie ou à toute autre forme de sens.

Maintenant que nous savons que la réalité est une relation syndifféonique linguistique autonome, même si nous semblons toujours la connaître d’un point de vue externe d’une manière plutôt non spécifique. Où devrions-nous aller ensuite à la recherche d’indices ? À ce stade, nous pourrions vraiment utiliser un MAP [NDT : une carte].

La Fermeture Syntactique : le Principe de l’Autologie Métaphysique (MAP)

Toutes les relations, modélisations et fonctions relatives à la réalité dans un sens effectif généralisé, qu’elles soient descriptives, définitives, compositionnelles, attributives, nomologiques ou interprétatives, sont générées, définies et paramétrées dans la réalité elle-même. En d’autres termes, la réalité comprend une « variété descriptive fermée » à partir de laquelle aucun prédicat essentiel n’est omis et qui ne contient donc aucune lacune critique qui ne laisse aucun aspect essentiel de la structure inexpliqué. Une telle lacune impliquerait la non-fermeture.

Diagramme 8

Le MAP, une amélioration théorique du critère d’auto-confinement défini par le Principe de Réalité, étend la propriété de fermeture de la définition de la réalité à l’ensemble de tous les prédicats réels. Le MAP effectue la fermeture sur les niveaux définitif, descriptif, explicatif et interprétatif de la théorie de la réalité en la transformant en un réseau fermé de définitions, descriptions, explications et interprétations couplées ne faisant référence à aucun élément extérieur à la réalité elle-même. Une autre façon de le dire est que le MAP, comme le principe de réalité, exige que tout ce à quoi toute définition, description, explication ou interprétation de la réalité-théorique se réfère soit situé dans la réalité. Cela a pour effet de rendre la réalité responsable de sa propre structure et de son évolution, au sens abstrait et concret.

Le MAP exige une explication sous forme fermée, au motif que la distinguabilité est impossible sans elle. Encore une fois, cela revient à la question de la stabilité syntactique.33 Pour l’exprimer de la manière la plus simple possible, la réalité doit ultimement posséder une distinction stable à deux valeurs au niveau objet, entre ce qui est et ce qui n’est pas, en maintenant les frontières informationnelles nécessaires entre les objets, les attributs et les événements. L’existence de frontières informationnelles fermées au sein d’un système n’est finalement possible que grâce à la fermeture systémique dans une composition dualiste (explanans-explanandum), ce qui est exactement ce qui se produit dans la logique sententielle.

Comme exemple de la nature tautologique du MAP, considérons une échelle externe hypothétique de distance ou de durée en fonction de laquelle la taille ou la durée absolue de l’univers ou de son contenu peut être définie. En raison de l’autonomie analytique de la réalité, les fonctions et définitions composant sa variété auto-descriptive ne se réfèrent qu’entre elles-mêmes; tout ce qui n’est pas impliqué dans son réseau syntactique est non pertinent pour la structure et méconnaissable en interne, tandis que tout ce qui est pertinent est déjà un ingrédient implicite du réseau et ne doit pas être importé de l’extérieur. Cela implique que si l’échelle proposée est pertinente, elle n’est pas vraiment externe à la réalité; en fait, la réalité la contient déjà comme une implication de sa structure intrinsèque.

En d’autres termes, puisque la réalité est définie sur la pertinence mutuelle de ses parties et aspects essentiels, externe et non pertinent sont synonyme; si quelque chose est extérieur à la réalité, alors il n’est pas inclus dans la syntaxe de la réalité et est donc méconnaissable en interne. Il s’ensuit que par rapport à ce niveau de réalité défini en termes de pertinence et de reconnaissance, il n’existe pas d’échelle « réelle mais externe » et que l’univers est donc extérieurement indéfini pour toutes les mesures, y compris la taille et la durée globale. Si une échelle absolue devait jamais être reconnue intérieurement comme une nécessité ontologique, cela impliquerait simplement l’existence d’un niveau de réalité plus profond auquel l’échelle est intrinsèque et par lequel elle est elle-même intrinsèquement expliquée comme fonction relative d’autres ingrédients. Ainsi, si le besoin d’une échelle absolue devenait reconnaissable dans la réalité – c’est-à-dire reconnaissable pour la réalité elle-même – il serait par définition relatif en ce sens qu’il pourrait être défini et expliqué en termes d’autres ingrédients de la réalité. En ce sens, le MAP est un « principe général de relativité ».34

Le critère « sans lacunes » du MAP ne permet pas de trous d’explication critiques omettant un quelconque aspect essentiel de structure. Ce que cela signifie peut être mieux illustré au moyen d’une erreur récurrente: « L’existence de l’univers est donnée et n’a donc pas besoin d’explication ». La phrase est donnée est incomplète; elle a des « choses à régler » cachées correspondant à ce par quoi l’existence est donnée, les moyens par lesquels elle est donnée et la raison pour laquelle elle est donnée. Si la source, les moyens et la raison sont effectivement réels, ils sont alors à l’intérieur de la réalité et le vide explicatif n’existe que dans l’esprit du demandeur plutôt que dans le réseau auto-explicatif de la réalité elle-même.

D’autre part, l’omission de cette phrase (est donnée) a pour résultat quelque chose comme « l’existence de l’univers est inexplicable ». Cela revient toutefois à affirmer que l’univers n’a pas de base ou de support d’existence identifiable, pas même lui-même… c’est-à-dire qu’aucune fonction explicative ne peut être définie sur l’explandandum et qu’il est en quelque sorte interdit à l’univers de servir comme sa propre source, moyen, ou raison. Mais cela revient à dire que l’univers ne peut exister que « par magie », surgissant de l’Apeiron avec une spontanéité dépassant celle par laquelle un véritable magicien pourrait tirer un lapin magique d’un chapeau. Alors que l’on peut au moins dire que les lapins magiques ont pour origine la magie associée à des magiciens qui les tirent des chapeaux hauts-de-forme vers la lumière de la réalité, ou se lancent comme par magie dans leurs propres chapeaux de leur propre réalité, l’univers serait privé de toute base ontologique ou de quelque support que ce soit… même d’une amorce.

Parce que des questions telles que « pourquoi et comment la réalité existe-t-elle (dans le domaine du potentiel existentiel soutenant la possibilité d’existence) ? » Et « pourquoi cette réalité existe-t-elle plutôt qu’une autre réalité ? »35 concernent les niveaux ontologiques ou téléologiques de la structure de la réalité et parce que ces niveaux de structure ont une signification logique, ils doivent avoir des réponses… même si ces réponses sont déterminées, comme le sont certaines d’entre elles, par le critère de fermeture lui-même.

Nous savons maintenant que la définition fermée du Principe de Réalité reposant sur un seul prédicat est en réalité une variété descriptive fermée de définitions liées contenant en principe les moyens de sa propre composition, attribution, reconnaissance, traitement et interprétation. Mais cela reste quelque peu automatonique. Qu’en est-il de l’esprit ? Puisque c’est par notre esprit que nous comprenons tout, la compréhension reste incomplète jusqu’à ce que nous en comprenions davantage sur la relation entre l’esprit et la réalité. Ainsi, après nous être équipés d’un MAP, nous nous occupons maintenant de la correspondance entre le MAP et le terrain.

Compréhensivité-réflexivité syntactique : le Principe Mind Equals Reality (M = R)

Le principe M = R ou Mind Equals Reality affirme que l’esprit et la réalité sont en définitive inséparables dans la mesure où ils partagent des règles communes de structure et de traitement. L’existence d’une relation de différence entre l’esprit et la réalité présuppose de manière syndifféonique un support relationnel ayant les caractéristiques des deux, ce support ayant la priorité logique sur la relation de différence elle-même.

Diagramme 9 : Principe M = R (Esprit = Réalité). Dans le diagramme syndifféonique ci-dessus, l’esprit est juxtaposé à la réalité dans un espace délimité par une boîte. La ligne séparant l’esprit et la réalité représente la différence supposée entre eux, tandis que l’intérieur de la boîte représente leur comparabilité ou leur « parenté » (ou, plus techniquement, leur syntaxe de différenciation uniforme ou unisecte, désignée par le foncteur U). L’extensionalité de la ligne est simplement celle de la boîte; sans la boîte, il n’y aurait pas de support d’extension pour contenir la ligne, ni aucun moyen d’exprimer la relation de différence associée. Parce que la séparation ne peut pas exister sans un support commun incorporant une syntaxe différentielle qui se distribue sur les deux retours de la relation de différence, la « séparation absolue » de l’esprit et de la réalité n’a pas de modèle… et sans modèle, la prémisse du dualisme esprit-matière cartésienne échoue. Cela indique que la réalité et l’esprit, l’information et le processeur d’information doivent finalement être considérés comme un tout. Toute distinction de style cartésien entre eux doit être strictement qualifiée.

Le principe M = R n’est simplement qu’une version logique de ce que les philosophes empiristes ont souligné il y a longtemps : nous faisons l’expérience de la réalité sous la forme de perceptions et de données sensorielles à partir desquelles l’existence et l’indépendance de l’esprit et la réalité extérieure objective sont induites. Comme toute preuve du contraire serait nécessairement cognitive, comme le sont toutes les « preuves », et puisque le contenu de la cognition est cognitif par intégration, une telle preuve ne peut exister; une telle preuve saperait son propre support et s’annulerait de ce fait. D’autre part, le Principe de Réalité dit que la réalité est autonome en ce qui concerne la reconnaissance et le contrôle, et dans la mesure où la reconnaissance et le contrôle sont « mentaux » (dans le sens où ils sont effectués conformément à la syntaxe cognitive et perceptuelle), la réalité l’est aussi. Le Principe M = R implique l’exhaustivité en définissant toutes nos perceptions, ainsi que leur infrastructure cognitive-syntactique au niveau syntaxique, comme des éléments de la réalité, indépendamment de la décidabilité.36 Quand il s’agit de M = R, il est difficile de résister à un petit jeu de mots : M = R dit qu’au niveau syntactique de la cognition et de la perception, « le MAP est le terrain ». Notez que M = R dépasse le simple isomorphisme kantien entre la réalité phénoménale et les catégories de pensée et de perception; il dit que la syntaxe et son contenu sont liés de manière récursive et, conjointement avec le Principe de Réalité, que tout supposé « contenu » non lié aux règles de structure et d’évolution de la réalité est sans pertinence. (Même s’il s’agit là d’une observation triviale dans la mesure où « non liées » et « non pertinentes » sont synonymes, il semble qu’il ait été largement ignoré par beaucoup de ceux qui auraient dû le savoir.)

En d’autres termes : si la partie « nouménale » (perceptuellement indépendante) de la réalité n’était vraiment pas liée à la partie phénoménale (cognition-isomorphe), alors ces deux « moitiés » de la réalité ne seraient ni coïncidentes ni partagées par un support les reliant. Dans ce cas, elles se décomposeraient tout simplement, et toute « réalité » intégrée les contenant supposément toutes les deux, échouerait faute de modèle intégré. Là où M (esprit) est identifié à la cognition et R (réalité) à des informations incarnées physiquement, M = R dit que la réalité consiste partout en une substance commune, l’infocognition, ayant la double nature de l’esprit et de la réalité (informationnelle).

La propriété M = R reprend là où le Principe de la Réductibilité Linguistique s’arrête en éliminant la distinction entre théorie et univers. Par ses lumières, la description théorique de la réalité par des êtres humains contenus dans la réalité revient à la réalité se décrivant elle-même. (Gardant à l’esprit qu’une théorie est une construction mentale, cela peut être illustré en remplaçant simplement Esprit et Réalité dans le diagramme ci-dessus par Théorie and Univers, et Esprit U Réalité par ThéorieU Univers.) Cela rend donc la théorie suffisamment réflexive et donc assez inclusive par définition pour décrire tout l’univers, y compris ce qui est rationnel, abstrait et subjectif, et ce qui est empirique, concret et objectif. La dissolution de cette distinction peut être considérée comme une réduction.

Nous savons donc maintenant que la réalité est plus qu’une relation syndifféonique linguistique autonome comprenant une variété descriptive fermée de définitions liées contenant les moyens de sa propre configuration, composition, attribution, reconnaissance, traitement et interprétation. C’est aussi une théorie d’auto-traitement identique à son univers.

Cohérence et consistance syntactiques : le Principe d’unité multiplexe (MU)

L’univers contient topologiquement ce qui contient l’univers de manière descriptive. MU, la configuration informationnelle minimale et la plus générale de la réalité, définit la relation entre l’unité et la multiplicité, l’univers et ses contenus bigarrés. À travers sa structure, l’univers et son contenu sont mutuellement inclusifs, se fournissant l’un l’autre un support.

En d’autres termes, nous pouvons caractériser de manière équivalente le contenu de l’univers comme topologiquement « à l’intérieur » de celui-ci (inclusion topologique) ou caractériser l’univers comme descriptivement « à l’intérieur » de son contenu, en occupant leurs syntaxes internes en tant qu’état acquis (inclusion descriptive). L’univers inclut de manière générique son contenu en lui servant d’unisecte syntactique, tandis que le contenu contient l’univers dans un sens plus spécifique impliquant des antécédents d’événements spécifiques qui se « mêlent » à l’interaction. Du premier point de vue, la cohérence syntactique du support global impose la consistance mutuelle des contenus, tandis que du second point de vue, les syntaxes cohérentes de son contenu contiennent, reconnaissent et transforment constamment le support. Ainsi, l’univers applique sa propre consistance grâce à la double maîtrise de soi. Ainsi, l’univers applique sa propre consistance à travers un double auto-confinement.

Diagramme 10 : Dans le diagramme syndifféonique [Diagramme 6], nous pouvons voir clairement le confinement des objets par le support, mais nous ne pouvons pas voir le confinement du support par les objets. Gardant à l’esprit que les termes de syntaxe et le contenu sont dans une certaine mesure des désignations relatives, le nœud supérieur du diagramme 10 correspond au support global (unisecte syntactique globale ou « métasyntaxe » de la réalité), tandis que le nœud inférieur correspond aux objets qui s’y trouvent (opérateurs syntactiques contenus dans le support); chacun est une unité multiplexe. La cohérence passe de la syntaxe globale au contenu local par le biais d’un confinement topologique global, ce qui applique l’unité à travers différents endroits et revient à la syntaxe globale dans plusieurs flux enchevêtrés générés par transduction croisée de contenu. La syntaxe devient état, et l’état devient syntaxe (où « syntaxe » s’entend comme englobant une distribution « ectosyntactique » d’opérateurs syntactiques). L’univers reste donc cohérent et consistant au cours de l’évolution.

La MU exprime la symétrie syndifféonique de la syntaxe et du contenu au niveau spatiotemporel de la réalité. Tout comme la syndifféonèse peut être considérée comme un paradoxe identifiant la différence avec la similitude, la MU peut être considérée comme une forme ultime de paradoxe identifiant la multiplicité et l’unité spatiotemporelle (le diagramme de MU est un éclaté du diagramme des relations syndifféoniques dans lequel la dimension de stratification est scindée en volets descriptifs et topologiques ou « dimensions temporelles »). La structure de MU résout le paradoxe de MU in situ par une stratification double, fournissant ainsi la fermeture, tandis que la stratification informationnelle ouverte de la théorie des types ne le peut. Parce que la MU peut ainsi être considéré comme la résolution du paradoxe décrit, sa signification, comme celui de la syndifféonèse, peut être exprimé comme suit : la réalité est un paradoxe auto-résolvant.

La MU, d’ailleurs, ne doit pas nécessairement être considérée comme le garant ultime de la consistance; cet honneur peut sans risque aller à la stabilité de la réalité perceptuelle elle-même. Tout simplement, la stabilité syntactique de la réalité prime sur toutes les objections concernant les limites des systèmes formels. La MU décrit simplement comment la réalité, considérée comme une théorie réflexive du SCSPL, atteint la stabilité intrinsèque au cours de son évolution. Ainsi, elle ne fonctionne pas comme un algorithme garanti de terminer sur la consistance mais pas sur l’inconsistance et n’est donc pas en conflit avec l’indécidabilité. La stabilité de la réalité affirme sa consistance, qu’une quelconque théorie inférieure apparaisse comme consistante ou non.

La MU sert de concept unificateur pour un ensemble d’idées relatives à la cohérence et à la consistance dans le contexte de la réalité théorique, comprenant l’hologie et plusieurs principes de dualité du CTMU.

Le Principe de l’Hologie (Auto-composition)

L’hologie, une analogie logique de l’holographie caractérisant la relation la plus générale entre la réalité et son contenu, est une forme d’auto-similarité dans laquelle la structure globale de l’univers est partout distribuée en tant que syntaxe acceptante et transductive, aboutissant à un support syntactique homogène. C’est-à-dire que, puisque la réalité exige une syntaxe constituée de lois générales de structure et d’évolution, et qu’il n’y a que la réalité elle-même pour servir cet objectif, la réalité comporte sa propre syntaxe auto-distribuée dans la MU (qui caractérise la relation globale entre syntaxe et contenu).

La propriété d’hologie elle-même est distribuée sur la réalité. C’est-à-dire que la frontière informationnelle d’un objet cohérent (opérateur syntactique) est multiplexée hologiquement par rapport à l’état (attribut et valeur) afin de définir l’intérieur descriptif de l’opérateur tandis qu’il participe à un auto-traitement global sans entrée. Ce multiplexage de possibilités n’est que la réplication de la structure de la frontière sur l’intérieur de la frontière en tant que fonction de temps. Encore une fois, l’opérateur n’a finalement rien d’autre pour exprimer sa capacité spatio-temporelle.

L’hologie est impliquée par le MAP car la réalité est fermée en composition et attribution; elle est impliquée par M = R car la réalité est composée d’opérateurs syntactiques à fonctionnalité mentale ou cognitive généralisée; et elle est impliquée par la syndifféonèse et la MU parce que c’est une expression de la relation entre le support spatio-temporel global et son contenu.

Les Principes de Dualité

La dualité est un concept omniprésent en mathématiques, apparaissant dans des domaines allant de la logique et de la théorie des catégories à la géométrie et à l’analyse. La relation de dualité est symétrique; si la dualisation de la proposition A produit la proposition B, alors la dualisation de B produit A. En géométrie projective, par exemple, l’opération de dualisation consiste à permuter les termes « point » et « ligne » dans les propositions qui les contiennent, comme dans « Deux points non coïncidents déterminent une ligne » LdualiseR « Deux lignes non parallèles déterminent un point. » Réaffirmer cela en « les lignes sont des fonctions de points » LdualiseR « les points sont des fonctions de lignes » révèle une relation de dualité entre fonctions et arguments. Ainsi, en algèbre vectorielle, le double espace V* d’un espace vectoriel V est l’espace de toutes les fonctions linéaires sur V (c’est-à-dire toutes les applications linéaires de V à R), tandis que V** est l’espace de toutes les applications linéaires de V* à R.

Une forme encore plus frappante de dualité est rencontrée dans la théorie des graphes, où le graphe double d’un graphe planaire transforme les faces en sommets et les sommets en faces sans perturber le motif global des adjacences. La frontière de chaque face est remplacée par des arêtes transversales convergeant sur son sommet double (et inversement), et la relation d’adjacence est redéfinie en conséquence. Lorsque les arêtes sont interprétées temporellement, des transformations intéressantes peuvent survenir; par exemple, les circulations le long des frontières faciales deviennent des « sommets de spin », et le mouvement le long d’un bord peut être caractérisé comme une opération entre les faces doubles de ses extrémités.

Les principes de la dualité se présentent ainsi sous deux variétés communes, l’une transposant relations spatiales et objets, et l’autre transposant objets ou relations spatiales et modélisations, fonctions, opérations ou processus. Le premier est appelé dualité espace-objet (ou E-O, ou ELRO); la seconde, la dualité temps-espace (ou T-E/O ou TLRE/O). Dans les deux cas, la caractéristique centrale est une transposition d’élément et une relation (spatiale ou temporelle) d’éléments. Ensemble, ces dualités s’ajoutent au concept de trialité, qui représente la possibilité universelle de permuter de manière consistante les attributs temps, espace et objet vis-à-vis de diverses structures. De là, nous pouvons extraire un troisième type de dualité: la dualité ET-O. Dans ce type de dualité, associée à ce que l’on appelle une dualité conspansive, les objets peuvent être « dualisés » aux transducteurs spatio-temporels, et l’univers physique est « simulé » intérieurement par ses contenus matériels.

M = R, MU et hologie sont tous au moins partiellement basés sur la dualité.

Le Principe de la Dualité Attributive (Topologique-Descriptive, État-Syntaxe)

Lorsque les points appartiennent à des ensembles et que les lignes sont des relations entre points, une forme de dualité est également valable entre ensembles et relations ou attributs, et donc entre théorie des ensembles et logique. Lorsque les ensembles contiennent leurs éléments et attributs décrivant leurs arguments de manière distributive, cela implique une double relation entre le confinement topologique et l’attribution descriptive, telle que modélisée à l’aide de diagrammes de Venn. Essentiellement, toute relation de confinement peut être interprétée de deux manières : en termes de position par rapport aux lignes de démarcation, surfaces ou hypersurfaces, comme dans la topologie d’ensemble de points et ses raffinements géométriques (⊃T), ou en termes de relations de distribution descriptives, comme dans la grammaire Venn-diagrammatique de la substitution logique (⊃D).37

La dualité attributive ou TD se reflète dans le fait que les ensembles et la logique sont décrits par la même structure algébrique, l’algèbre booléenne, qui exprime leur double relation dans la relation entre ses deux opérations. Exprimées en termes de théorie des ensembles, ces opérations sont l’union et l’intersection (∪, ∩); en termes logiques, ils sont OU et ET (∨, ∧).(∪, ∩) et (∨, ∧) sont liés comme suit : l’union (A∪B) de deux ensembles A et B est constituée de tous et uniquement les éléments appartenant soit à A, soit à B ou aux deux (∀x ∈A∪B: x ∈A ∨ x ∈B), alors que l’intersection (A∩B) de A et B est constituée de tous et uniquement les éléments appartenant à la fois à A et à B (∀x ∈A∩B: x ∈A ∧ x ∈B). Ce genre de dualité est bien connu; elle a trait au fait que tout énoncé attributif définissant une relation de prédicats peut être reformulé comme un énoncé concernant des ensembles (et inversement).

Mais la relation entre la théorie des ensembles et la logique est encore plus intéressante que cela, car chacune a une affinité représentationnelle particulière pour une seule de ces opérations. C’est-à-dire que la théorie des ensembles a tendance à se concentrer sur les objets (ensembles et éléments), tandis que la logique tend à se concentrer sur les attributs ou sur les « contraintes de frontière » informationnelles que les objets doivent satisfaire. Ainsi, la théorie des ensembles définit ultimement les ensembles en fonction des objets qu’ils contiennent, tandis que la logique tend à les définir « de l’extérieur vers dedans » sur les contraintes de frontières entrecoupées auxquelles ils se conforment. La différence repose sur le foncteur univalent non (~), sur lequel la complémentation et l’intersection, mais non l’union, sont directement ou indirectement définies.

Par exemple, s’il est assez facile d’identifier un élément individuel ou un ensemble en le nommant de manière constructive ou en « l’énumérant », par ex. « X », l’identification de son complément nécessite souvent que son nom soit utilisé comme base d’une contrainte restrictive pouvant être appliquée à l’ensemble d’un contexte fini ou infini dans une opération d’attribution, par ex. « non-X ». La relation de dualité qui tient entre noms et contraintes est joliment capturée par les lois de De Morgan, ~A∩ ~B= ~(A∪B) et ~A∪ ~B= ~(A∩B), qui l’expriment en permutant l’objectif et opérations attributives ∪ et ∩.

Étant donné que les états s’expriment topologiquement alors que les structures syntactiques de leurs opérateurs sous-jacents s’expriment de manière descriptive, la dualité attributive est parfois appelée dualité état-syntaxe. Les informations nécessitant une organisation syntactique, cela revient à évaluer la syntaxe cognitive/perceptuelle; inversement, la reconnaissance consiste en une restriction soustractive du potentiel informationnel par une acquisition additive d’informations. La dualité TD relie donc l’information au potentiel informationnel lié par la syntaxe et la perception (acquisition d’état cognitif) à la cognition.

Dans un diagramme de Venn, le contenu des cercles reflète la structure de leurs frontières; les frontières sont les descripteurs primaires. L’intérieur d’un cercle est simplement une « intériorisation » ou une auto-distribution de sa « contrainte de frontière » syntactique. Ainsi, les cercles imbriqués correspondant à des objets identiques affichent une forme descriptive de confinement correspondant à une stratification syntactique, avec des niveaux sous-jacents correspondant à des recouvrements syntactiques.

Cela conduit à une forme liée de dualité, la dualité constructive-filtrante.

La Dualité Constructive-Filtrante

Tout ensemble pouvant être construit en ajoutant des éléments à l’espace entre deux crochets peut être défini par une restriction de l’ensemble de tous les ensembles possibles. La restriction implique la superposition de type Venn de contraintes de nature soustractive; ainsi, cela ressemble à un processus de couleur soustractive impliquant l’empilement de filtres. Les éléments, en revanche, sont additifs et le processus de construction d’ensembles est donc additif; cela ressemble à un processus de couleur additif impliquant l’éclairage des éléments de couleur des pixels dans un moniteur couleur. La dualité CF affirme simplement l’équivalence générale de ces deux types de processus par rapport à la réalité logico-géométrique.

La dualité CF capture les ramifications temporelles de la dualité TD, reliant les opérations géométriques sur des ensembles de points à des opérations logiques sur prédicats. Essentiellement, la dualité CF dit que tout état géométrique ou transformation continue équivaut à une opération impliquant la « filtration » mutuelle d’intersection de potentiels d’état hologiques. Les états et objets, au lieu d’être construits à partir du niveau d’objet, peuvent être considérés comme des raffinements filtrants de relations d’ordre supérieures générales, non spécifiées intérieurement.

La dualité CF est nécessaire pour montrer comment un univers peut être à « somme nulle »; sans cela, il est impossible d’affiner les conditions objectives des processus constructifs « à partir du néant ». Dans la cosmogonie du CTMU, le « néant » est défini informellement comme une contrainte zéro ou une liberté pure (télèse non bornéeou UBT), et la construction apparente de l’univers est expliquée comme une auto-restriction de ce potentiel. Dans un domaine de potentiel ontologique non borné, définir une contrainte n’est pas aussi simple que de simplement l’écrire; parce que les contraintes agissent de manière restrictive sur le contenu, la contrainte et le contenu doivent être définis simultanément dans une relation syntaxe-état unifiée.

La Dualité Conspansive

Ce principe a été dans une certaine mesure résumé par la citation apocryphe suivante, attribuée à Arthur Eddington38, concernant l’univers en expansion :

« Nous marchons sur la scène de la vie, interprètes d’un drame au profit du spectateur cosmique. Au fur et à mesure que les scènes se déroulent, il remarque que les acteurs sont de plus en plus petits et l’action plus rapide. Lorsque le dernier acte s’ouvre, le rideau se lève sur les acteurs nains se précipitant dans leurs rôles à une vitesse effrénée. De plus en plus petit. De plus en plus vite. Un dernier flou microscopique d’intense agitation. Et puis rien. »

La vision surréaliste d’Eddington s’accompagnait d’une proposition ironique qui voulait que la théorie de l’univers en expansion soit remplacée par une théorie de « l’atome rétrécissant ». C’était donc un peu exagéré pour des raisons d’humour. En effet, Eddington n’était pas suffisamment intéressé par l’idée pour développer ses implications au-delà d’un niveau très rudimentaire. Cependant, il s’avère qu’il traçait les contours d’un principe de dualité important.

L’expansion cosmique et le mouvement physique ordinaire ont quelque chose en commun : ce sont tous les deux ce que l’on pourrait appeler des ectomorphismes. Dans un ectomorphisme, quelque chose est modélisée, générée ou répliquée dans quelque chose d’extérieur à elle. Cependant, le Principe de Réalité affirme que l’univers est autonome sur le plan analytique et que l’ectomorphisme est inconsistant avec l’autonomie. Par le principe de la dualité conspansive, l’ectomorphisme est associé à l’endomorphisme, selon lequel les choses sont modélisées, générées ou répliquées en elles-mêmes. Grâce à l’endomorphisme conspansif, les objets syntactiques sont modélisés par injection dans leurs propres intérieurs hologiques à partir de leurs propres frontières syntactiques.

Dans le langage de la dualité TD et CF, cela déplace l’accent mis sur la géométrie espace-temps au lieu du confinement descriptif, et du traitement constructif au filtrant. En conséquence, de nouveaux états sont formés dans les images des états précédents. Rien ne bouge ni ne se développe « à travers » l’espace; l’espace est un état, et chaque déplacement d’un objet n’est qu’un mouvement d’un niveau de stase parfait à un autre. Cela lie le mouvement conventionnel, dans lequel les lignes du monde sont créées de manière constructive par des ajouts d’état dans les diagrammes de Minkowski, à l’endomorphisme différentiel, dans lequel les potentiels descriptifs internes des attributs sont restreints de manière cumulative.

Un diagramme espace-temps (Minkowski) est une sorte de « réseau d’événements » dans lequel les nœuds représentent des événements et leurs lignes connectives représentent les objets qui interagissent dans ces événements. Les événements se produisent aux foyers de cônes de lumière passés et futurs auxquels les lignes du monde sont internes. Si vous pouviez regarder l’axe temporel d’un tel diagramme à une section transversale semblable à celle d’un espace, vous verriez quelque chose qui ressemblerait beaucoup à un diagramme de Venn avec des cercles correspondant à des sections transversales de cônes de lumière. Cette rotation du diagramme correspond à une dualisation conspansive convertissant un réseau spatio-temporel de lignes du monde et d’événements en une série stratifiée de diagrammes de Venn.

Diagramme 11 : Dans l’illustration ci-dessus, une coupe transversale spatiale d’un diagramme espace-temps (ligne bleue) est tournée vers le spectateur et affichée le long de l’axe du temps (rectangle bleu). Le résultat est un diagramme de Venn dans lequel les cercles représentent des objets et des événements, ou des relations interactives (n>1)-aires d’objets. C’est-à-dire que chaque cercle décrit les « fonctions d’onde quantiques intriquées » des objets qui ont interagi les uns avec les autres pour le générer. Les petits points au centre des cercles représentent les événements et objets initiaux à partir desquels les cercles sont apparus, tandis que les points jumeaux où les cercles se chevauchent reflètent le fait que tout nouvel événement possible, ou toute interaction entre des objets impliqués dans les anciens événements, doit se produire par acquisition mutuelle dans l’intersection. La croissance extérieure (ou par dualité conspansive, l’absorption mutuelle) des cercles est appelée expansion interne, tandis que l’effondrement de leurs objets lors de nouveaux événements est appelé requantification. Les cercles eux-mêmes sont appelés DEI, abréviation de domaines étendus internes, et correspondent à des paires d’opérateurs syntactiques interactifs impliqués dans des événements de perception généralisée (notez « l’évacuation » hologique et l’absorption mutuelle des opérateurs). L’espace-temps peut être illustré en termes de stratification de tels diagrammes de Venn, le contact mutuel étant appelé « superposition étendue » (dans le monde réel, les diagrammes de Venn sont tridimensionnels plutôt que plans, les cercles sont des sphères et « stratification » est défini en conséquence). La superposition étendue « atemporellement » répartit les événements antécédents sur les événements ultérieurs, plaçant ainsi l’espace-temps dans un auto-contact temporellement étendu. À la lumière du Principe Télique (voir ci-dessous), ce scénario implique une nouvelle interprétation de la théorie quantique, la somme sur avenirs. La somme sur avenirs implique une généralisation atemporelle du « processus », la récursion télique, par laquelle l’univers effectue la maximisation à la volée d’un paramètre global d’auto-sélection, l’utilité généralisée.

Dans un diagramme de Venn, les cercles représentent les ensembles à travers leurs attributs définitifs. Les attributs représentés par les cercles sont synétiques (distribués syntactiquement et homogènes vis-à-vis des différences potentielles d’état), et l’attribut représenté par un cercle particulier est uniformément héritable par les éléments de l’ensemble représentés par tout cercle à l’intérieur de celui-ci. Dans le diagramme de Venn spatio-temporel que nous venons de décrire, les sections transversales des cônes de lumière circulaires correspondent à des objets et à des événements se rapportant de la sorte. Etant donné que les objets à l’échelle quantique ne sont vus exister que lorsqu’ils participent à des événements d’observation, y compris leurs « observations généralisées », leurs lignes du monde sont simplement supposées exister entre événements et sont en fait rétrodictées syntactiquement, avec le continuum, depuis les derniers événements auxquels ils sont connus pour avoir participé. Cela permet d’omettre complètement des lignes du monde spécifiques, en les remplaçant par une série de diagrammes de Venn dans lesquels les cercles se développent intérieurement, s’interpénètrent et se « réduisent à des points » lors de chaque événement d’observation généralisé interactif. Ce scénario est général, s’appliquant même aux objets macroscopiques constitués de nombreuses particules de matière; la définition plus élevée des lignes du monde des objets macroscopiques peut être imputée à une fréquence d’effondrement plus élevée en raison de la densité interactive entre leurs particules constitutives.

Les zones situées à l’intérieur des cercles correspondent aux potentiels d’événements et, aux cas où les événements sont régis par les lois de la physique, aux instanciations potentielles de la loi physique ou de la « syntaxe nomologique ». Lorsque chaque cercle correspond à deux objets ou plus, il comprend également les potentiels d’objet. En d’autres termes, les limites circulaires des cercles de Venn peuvent être interprétées comme celles d’objets « potentialisés » en train d’absorber leurs voisinages spatio-temporels. Puisque les potentiels d’événements et les potentiels d’objet coïncident, on peut dire que les instanciations potentielles de loi résident « à l’intérieur » des objets et peuvent donc être considérées comme des fonctions de leurs règles internes ou de « syntaxes d’objet ». Les objets deviennent ainsi des opérateurs syntactiques, et les événements deviennent des intersections de la syntaxe nomologique dans la valeur commune d’un paramètre d’état observable, la position. Le cercle correspondant au nouvel événement représente un attribut constitué de toutes les relations nomologiques associées appropriées à la nature de l’interaction, y compris les agrégats conservés, et forme un « recouvrement syntactique » point par point (au niveau des états) pour tous les potentiels ultérieurs.

Notez que dans ce scénario, l’espace-temps évolue linguistiquement plutôt que géométriquement. Bien que chaque cercle de Venn semble s’étendre continuellement, son contenu reste inchangé; son attribut associé reste statique en attente d’événements ultérieurs impliquant les objets qui l’ont créé. Étant donné que rien ne change réellement jusqu’à ce qu’un nouvel événement soit « substitué » à l’événement précédent, c’est-à-dire jusqu’à ce qu’un nouveau cercle apparaisse dans l’ancien par intégration syntactique, les cercles ont une durée intrinsèquement indéfinie et sont donc intrinsèquement atemporels. Le temps apparaît strictement comme une relation ordinale entre les cercles plutôt qu’au sein même des cercles. En ce qui concerne les éléments de syntaxe invariants dans le temps, actifs dans un état donné (le cercle), la distinction entre durée nulle et non nulle est intrinsèquement dépourvue de sens; de tels éléments sont héritables par substitution et deviennent des ingrédients syntactiques des états ultérieurs. Étant donné que chaque cercle est structurellement auto-distribué, rien ne doit être transmis d’une partie à une autre; les contraintes de localité ne surviennent que par rapport à des invariants supplémentaires activés de manière différentielle dans des cercles représentant des états ultérieurs et brisant la symétrie hologique de leurs antécédents. La conspansion procure donc un certain soulagement aux problèmes liés à la « non-localité quantique ».

Parce que le rétrécissement d’un objet dans son image antérieure équivaut à une forme de substitution logique dans laquelle l’objet est « décrit » par un diagramme de Venn ou déterminé par son état antérieur, il n’y a aucun moyen de distinguer entre l’expansion systémique externe et la substitution de contenu vers l’intérieur , ou entre les « grammaires » dynamiques et logiques associées. Ceci est simplement une reformulation de la dualité attributive; les relations de confinement topologiques entre ensembles de points sont équivalentes à la prédiction descriptive de la vérité des déclarations affirmant le confinement et aux relations de distribution entre descripteurs d’état. En conjonction avec la symétrie intrinsèque des systèmes extérieurs indéfinis, la dualité attributive élimine toute distinction logique ou géométrique possible entre l’expansion extérieure d’un univers autonome, son contenu demeurant statique en taille, et un endomorphisme logique dans lequel l’univers reste statique tandis que les états de son contenu sont substitués de manière récursive aux états précédents.

En ce qui concerne le MAP, il a déjà été noté que, lorsque les dimensions extérieures d’un système sont indéfinies, aucune distinction de taille ne peut être faite au-delà du rapport de taille du système à son contenu. Considérons une simple analogie arithmétique : 1/2 = 1000/2000 = 1(109999)/2(109999) = (…). Lorsque le numérateur et le dénominateur d’une fraction sont tous deux multipliés par un nombre donné, la valeur de la fraction ne change pas; elle est indépendante des distinctions impliquant la taille du multiplicateur. Similairement, la proportionnalité intrinsèque d’un système autonome est indépendante des distinctions impliquant une mesure externe. Cela implique que, dans le cas d’un univers autonome pour lequel il n’existe aucune mesure externe, aucune distinction ne peut être faite entre l’expansion du système par rapport à son contenu, et le rétrécissement de son contenu par rapport à lui. En fait, comme ce qui est indéfini ne peut changer – il n’existe pas de définition précise quant à laquelle un changement serait possible – l’expansion apparente du conteneur ne peut pas être définie de façon extrinsèque, mais implique un rétrécissement intrinsèque conspansivement équivalant de son contenu.

Ainsi, la dualité conspansive relie deux vues complémentaires de l’univers, l’une basée sur les états (relatifs) externes d’un ensemble d’objets et l’autre basée sur les structures internes et les dynamiques d’objets considérés comme des processeurs de langage. La première, qui représente l’univers tel qu’il est généralement compris en physique et en cosmologie, s’appelle ERSU, abréviation de Expanding Rubber Sheet Universe [NDT : univers de feuille de caoutchouc en expansion], tandis que le second s’appelle USRE (ERSU épelé à l’envers), abréviation de Universe as a Self-Representational Entity [NDT : univers en tant qu’entité auto-représentative]. Simplement, ERSU est comme un ensemble, spécifiquement un ensemble de points topologiques et géométriques, tandis qu’USRE est comme un langage nomologique auto-descriptif. Tandis qu’ERSU s’étend par rapport aux tailles invariantes de son contenu, USRE « se conspand », maintenant la taille de l’univers invariant tout en permettant aux tailles d’objets et échelles de temps de rétrécir dans des proportions mutuelles, préservant ainsi la covariance générale.

Cela a certaines implications intéressantes. Premièrement, alors qu’il est généralement supposé que la taille des objets matériels reste fixe alors que celle de tout l’univers se modifie « ectomorphiquement » autour d’eux, la conspansion maintient la taille de l’univers immuable et modifie de manière endomorphique celle des objets. Parce que l’univers joue maintenant le rôle d’invariant, il existe un taux standard global d’expansion interne ou d’absorption mutuelle entre les contenus de l’univers (« invariance c ») et, en raison de la covariance syntactique, les objets doivent être redimensionnés ou « requantisés » avec chaque nouvel événement selon un facteur de redimensionnement constant (indépendant du temps) résidant dans la syntaxe globale. Deuxièmement, comme le taux de rétrécissement est une fonction constante d’un rapport de taille changeant, l’univers apparaît, d’un point de vue interne, en train de s’accélérer dans son « expansion », ce qui conduit au double conspansif d’une constante cosmologique positive.39

La dualité conspansive, dont le rôle dans le CTMU est quelque peu analogue à celle du Principe d’Équivalence dans la Relativité Générale, constitue la seule échappatoire à une « tour de tortues » ectomorphique infinie. Si la géométrie perceptuelle de la réalité manquait d’une représentation conspansive double, tout mouvement nécessiterait un réseau spatial fixe ou un « arrière-plan spatial » ectomorphique nécessitant une explication propre, et ainsi de suite dans la tour. La conspansion permet à l’univers de s’auto-configurer par rétroaction temporelle. Chaque cercle conspansif représente un potentiel d’événement correspondant à une certaine combinaison de loi et d’état; même après que l’un de ces cercles intrinsèquement atemporels se soit « étendu intérieurement » à travers de vastes étendues d’espace et de temps, son événement source reste d’actualité pour tout ce qui interagit avec lui, par exemple un œil percevant l’un de ses photons. Dans le même temps, la conspansion confère à la fonction d’onde quantique des objets un nouveau foyer : à l’intérieur des objets conspansifs eux-mêmes. Sans elle, non seulement la fonction d’onde n’a pas de foyer, mais elle échoue à coïncider avec tout système de prédicats ou de « lois de la physique » évoluant logiquement. Éliminez la conspansion et la réalité devient un espace inexplicable rempli de lignes du monde déterministes et de la lourde charge de problèmes à laquelle on peut s’attendre lorsque la géométrie divorce de la logique.

Là où la réalité est caractérisée par un monisme infocognitif d’aspect double (comme vu), elle consiste en unités d’infocognition reflétant un couplage distribué de syntaxe transductive et de contenu informationnel. La conspansion décrit « l’alternance » de ces unités entre les aspects doubles (généralisés-cognitifs et informationnels) de la réalité, et donc entre la syntaxe et l’état. Cette alternance, qui permet des raffinements mutuels localisés de la syntaxe cognitive et de l’état informationnel, est essentielle au processus évolutif appelé récursion télique. La récursion télique requiert un autre principe basé sur la dualité conspansive, le Principe de Superposition Étendue, selon lequel les opérateurs peuvent être simultanément acquis par plusieurs télons, ou relations syntaxe-état spatiotemporellement étendues impliquant des opérateurs génériques dans des événements potentiels et guidant leur décohérence de manière opportuniste.

Notez que la conspansion explique la « flèche du temps » en ce sens qu’elle n’est pas symétrique en inversion. D’autre part, l’imbrication conspansive d’événements atemporels met tout le temps en « auto-contact simultané » sans compromettre l’ordinalité. La dualité conspansive peut être vue comme la conséquence d’un type de symétrie de jauge (mesure) par lequel seules les dimensions relatives de l’univers et de son contenu sont importantes.

Le Principe de Superposition Étendue

En mécanique quantique, le principe de superposition d’états dynamiques affirme que les états dynamiques possibles d’un système quantifié, comme les ondes en général, peuvent être superposés linéairement, et que chaque état dynamique peut ainsi être représenté par un vecteur appartenant à un espace vectoriel abstrait. Le principe de superposition permet de définir des « états mixtes » consistants en de nombreux « états purs » possibles, ou des ensembles définis de valeurs de paramètres d’état. Dans une telle superposition, les paramètres d’état peuvent avoir simultanément plusieurs valeurs.

Le principe de superposition met en évidence certains problèmes de la mécanique quantique. L’un des problèmes est que la mécanique quantique manque d’un modèle convaincant permettant d’interpréter des choses comme des « états mixtes » (les ondes seules ne suffisent pas). Un autre problème est que, selon le principe d’incertitude, les derniers états d’une paire de particules en interaction sont généralement insuffisants pour déterminer pleinement leurs prochains états. Cela soulève bien sûr une question : comment leurs prochains états sont-ils en fait déterminés ? Quelle est la source de la mesure supplémentaire décisive de détermination requise pour sélectionner leurs prochains événements (« effondrer leurs fonctions d’onde ») ?

La réponse n’est pas, comme certains pourraient le supposer, « l’aléatoire »; l’aléatoire équivaut à une causalité, ou bien à une incompressibilité informationnelle vis-à-vis de tout modèle causal distribué ou de tout ingrédient de la syntaxe causale. Ainsi, soit ce n’est pas une explication du tout, soit cela implique l’existence d’une « cause » dépassant la capacité représentative des lois de causalité distribuées. Mais, le premier cas est à la fois absurde et non scientifique, et le second cas exige que l’on tienne compte explicitement d’ordres de causalité plus élevés… plus que ce que l’on peut facilement discerner dans une simple invocation magique de « l’aléatoire ».

Le principe de superposition, à l’instar d’autres aspects de la mécanique quantique, repose sur l’hypothèse du Markovianisme physique.40 Il fait référence à des états mixtes entre événements adjacents, ignorant la possibilité de relations temporelles extensives non aléatoires, non entièrement attribuables à des lois distribuées. En mettant les événements temporairement éloignés en contact descriptif étendu les uns avec les autres, le Principe de Superposition Étendue permet une rétroaction télique trans-temporelle cohérente et joue donc un rôle nécessaire dans l’auto-configuration cosmique. Parmi les relations déterminantes d’ordre supérieur dans lesquelles des événements et des objets peuvent ainsi être impliqués, se trouvent des relations utiles d’état-syntaxe appelées télons, des attracteurs téliques capables de guider l’évolution cosmique et biologique.

Étant donné que la théorie quantique ne semble pas être irrévocablement attachée au Markovianisme, pourquoi la possibilité de relations causales d’ordre supérieur n’a-t-elle pas été sérieusement envisagée ? Une des raisons est la géométrie espace-temps, qui semble confiner les objets à des « lignes du monde » unidimensionnelles dans lesquelles leurs événements de transition d’état sont séparés par des segments intermédiaires qui les empêchent de « se mélanger » de manière globalement significative. C’est pour cette raison que la superposition n’est habituellement appliquée qu’aux transitions d’états individuels, du moins à ceux qui souscrivent à des interprétations conservatrices de la mécanique quantique.

La dualité conspansive, qui intègre les composants TD et CF, supprime cette restriction en plaçant les événements de transition d’état dans un contact descriptif direct. Comme les intervalles géométriques entre les événements sont générés et sélectionnés par un traitement descriptif, ils n’ont plus de force séparative. Cependant, comme les lignes du monde reflètent avec précision les lois distribuées en termes de transitions d’états exprimées, elles ne sont pas réduites au statut d’artefacts interpolés sans réalité dynamique; leurs qualités séparatives sont simplement remplacées par la dynamique syntaxique d’état de leur représentation conspansive double.

En élargissant le concept de superposition pour y inclure des relations non triviales d’ordre supérieur, le Principe de Superposition Étendue ouvre la porte au sens et à la conception. Parce qu’il soutient également les relations de distribution entre les états, les événements et les strates syntactiques, il fait de la cosmogonie un événement distribué, cohérent et continu plutôt qu’un moment passé et abandonné de l’histoire ancienne du cosmos. En effet, la justification habituelle de la participation d’un observateur – le fait qu’un observateur présent puisse faire s’effondrer perceptuellement les fonctions d’onde d’événements anciens (émission de photons) – peut être considérée comme une conséquence de cette relation logique.

Supertautologie

La vérité, un prédicat représentant l’inclusion dans un domaine, est la propriété logique en vertu de laquelle une chose peut être identifiée et distinguée d’une autre à n’importe quel niveau de résolution. Toutes les théories visent la vérité et la théorie de la réalité ne fait pas exception. En ce qui concerne la science, il y a un problème avec la vérité : au-delà du niveau d’observation directe, elle ne peut être certifiée par des moyens empiriques. Il faut blâmer diverses formes d’incertitude, l’ambiguïté de la théorie des modèles et le problème de l’induction : les généralisations scientifiques sont circulaires dans la mesure où elles reposent nécessairement sur l’hypothèse que la nature est uniforme. Le problème de l’induction limite effectivement la certitude au raisonnement mathématique.

Cela n’est guère surprenant, car la vérité est finalement un concept mathématique. En logique, la vérité est définie au moyen d’expressions toujours vraies appelées tautologies. Une tautologie logique possède trois propriétés distinctives : elle est descriptivement universelle, elle est fermée par une auto-composition récursive et elle est consistante intérieurement et extérieurement aux niveaux de référence syntactique et sémantique. Puisque la logique est la théorie de la vérité, la façon de construire une théorie entièrement vérifiable consiste à commencer par la logique et à développer la théorie au moyen de règles ou de principes sous lesquels la vérité peut être héritée. La vérité étant synonyme de tautologie logique, cela signifie développer la théorie en joignant des règles qui ont elles-mêmes une structure tautologique – c’est-à-dire universelles, fermées et consistantes – et en extrayant logiquement les implications. Une théorie de la réalité construite de cette manière s’appelle une supertautologie.

Dans une théorie supertautologique de la réalité, il est inutile d’assumer l’uniformité de la nature en ce qui concerne certains types de généralisation. Au lieu de cela, de telles généralisations peuvent être déduites mathématiquement… par ex. la covariance nomologique, l’invariance du taux d’autotraitement global (invariance c) et l’expansion du système en accélération apparente interne.

Réduction et Extension

Les plus grandes avancées théoriques ont généralement été associées à deux processus complémentaires, la réduction et l’extension. Les composants conceptuels d’une théorie sont réduits à des composants plus fondamentaux, et la théorie est étendue par l’émergence de relations nouvelles et plus générales entre eux. Le CTMU réduit la réalité à une information auto-transductive et finalement à la télèse, en utilisant la structure syntactique réflexive fermée de la première comme gabarit pour la théorie de la réalité.

En science, tout exige une explication… même les explications. Non seulement les observations exigent des théories explicatives, mais les théories exigent également leurs explications. Malheureusement, on oublie parfois que jusqu’à ce que quelque chose ait été expliqué de manière explicable, cela n’a pas du tout été correctement expliqué. Si une théorie ne s’explique pas d’elle-même, elle doit être réduite à une théorie plus fondamentale qui l’explique; sinon, elle repose simplement sur des hypothèses.

Par exemple, considérez une explication selon laquelle « les oiseaux peuvent voler parce qu’ils ont des ailes ». Sans explication de la résistance atmosphérique, cette explication est incomplète; elle ne contient aucune explication sur la raison ou la manière dont les ailes permettent le vol, se basant simplement sur l’hypothèse qu’elles le font. Par conséquent, bien que cela soit vrai jusque-là, cela laisse de côté les connaissances porteuses indispensables et ne peut tenir seul. En résumé, toute théorie Ti+1 qui ne s’explique pas d’elle-même doit être réductible à une théorie plus fondamentale Ti qui l’explique et la soutient, de sorte que Ti ⊨ Ti+1, et cette régression explicative ne peut se terminer que par une théorie auto-explicative T0.

Ce fait est très souvent oublié en biologie évolutive, où (par exemple) les détails de la structure et de la dynamique moléculaires sont utilisés pour expliquer les phénomènes organiques. Bien que ces détails proviennent des théories les plus fondamentales de la chimie et de la physique quantique, ils ne constitueront jamais une explication satisfaisante de la vie tant qu’ils n’incorporeront pas seulement une explication de la physique et de la chimie, mais aussi la réalité en général. Cela est vrai car la réalité physique (observable) n’est pas un modèle complet pour la physique et n’est donc pas autonome en ce qui concerne l’explication – en ce sens, toute interprétation exclusivement matérialiste de la théorie physique est prima facie absurde – et parce que la physique est une théorie non auto-explicative, quel que soit le modèle. Pour expliquer le phénomène organique à l’aide de la sélection naturelle, il est nécessaire d’expliquer la sélection naturelle, y compris la « sélection naturelle » des lois de la physique et de l’univers dans son ensemble.

La réduction théorique implique un délitement régressif des contraintes informationnelles progressives afin de parvenir à des explications de plus en plus élémentaires. Les signatures théoriques fermées sont déchirées et réduites à des concepts plus fondamentaux qui peuvent être reformés en signatures plus fondamentales et plus expressives. Cependant, la partie informationnelle de la régression se termine là où une réduction supplémentaire compromettrait l’intelligibilité; il ne peut plus y avoir de régression réductrice à travers des couches théoriques de plus en plus fondamentales une fois que les exigences de régression, de réduction, de théorisation et de stratification ont elles-mêmes été perdues. Au-delà de ce point, l’infocognition cède la place au potentiel informationnel et cognitif, ou télèse.

Le processus de réduction des distinctions au support syntactique homogène qui les prend en charge est appelé régression syndifféonique. Ce processus implique l’unisection, en vertu de laquelle les règles de structure et de dynamique qui gouvernent respectivement un ensemble d’objets distincts sont réduites à une « jonction syntactique » dans un réseau infocognitif de supports syntactiques. L’unisection est une forme générale de réduction qui implique que toutes les propriétés réalisées dans un support sont des propriétés du support lui-même.

Lorsque les propriétés émergentes ne sont que des propriétés latentes du support d’émergence téléo-syntactique, les mystères des phénomènes émergents sont réduits à deux : comment les propriétés émergentes sont-elles anticipées dans la structure syntactique de leur support d’émergence, et pourquoi ne sont-elles pas exprimées sauf dans conditions spécifiques impliquant (par exemple) le degré de complexité systémique ?

Le Principe de Monisme Infocognitif

Lorsque la langue est constituée d’informations et que l’information a une structure linguistique, le Principe de la Réductibilité Linguistique implique que l’information est aussi fondamentale que la langue. Dans la mesure où nous ne pouvons pas comprendre la réalité si ce n’est en termes théoriques (linguistiques, informationnels), cela nous permet de faire de la réalité un « langage à auto-traitant » ou un ensemble univers-théorie auto-définissant, auto-explicatif, auto-modelant, sans crainte de se tromper par une autre réduction théorique. Cependant, la réduction linguistique de la réalité est superficiellement macroscopique. Tout comme un langage parfaitement autonome doit être un auto-traitant (faute de quoi que ce soit d’extérieur pour le traiter), les informations qui le constituent doivent également l’être. Cela conduit au concept d’auto-traitement de l’informationet finalement à une théorie microscopique (quantique) de l’information.

Il est facile de montrer que l’information est auto-traitante. La structure est attributive; les parties de toute structure possèdent des attributs qui les positionnent ou les définissent autrement relativement aux autres parties. Pour être significative et donc informative, l’information doit être structurée; par conséquent, l’information doit posséder des attributs. Les relations attributives, intrinsèques ou autres, doivent être conformes aux règles logiques gouvernant l’attribution, c’est-à-dire à une syntaxe logique attributive incorporant les calculs propositionnels et prédicats. Ainsi, les informations ne peuvent exister que conjointement avec la syntaxe logique attributive. Du fait qu’elle incorpore nécessairement une syntaxe attributive, elle dispose d’une capacité d’auto-traitement native pour maintenir sa structure intrinsèque, ce qu’elle doit faire pour être qualifié d ’« informationnel ».

Parce que la cognition et la transduction d’information générique sont identiques jusqu’à l’isomorphisme – après tout, la cognition n’est que la forme spécifique de traitement de l’information qui se produit dans un esprit – le traitement de l’information peut être décrite comme « cognition généralisée » appelé infocognition. La réalité consiste donc en une seule « substance », l’infocognition, dont les deux aspects correspondent à la transduction et être transduit. Décrire la réalité comme une infocognition revient donc à un monisme à aspect double (infocognitif). Lorsque l’infocognition est égale à la distribution généralisée de l’auto-perception et de l’auto-cognition de la réalité, le monisme infocognitif implique une forme stratifiée de « panpsychisme » dans laquelle au moins trois niveaux d’auto-cognition peuvent être distingués en ce qui concerne la portée, le pouvoir et la cohérence : globale, agentive et subordonnée.

Finalement, le passage conceptuel de l’information à l’auto-transduction de l’information nécessite des extensions des théories à forte intensité d’information, notamment les théories de l’information, de la calculabilité et de la cybernétique. Le problème provient du fait que, comme il est compris dans ces domaines, l’information est un concept limité fondé sur un modèle d’ingénierie dans lequel l’existence d’expéditeurs, de récepteurs, de messages, de canaux et de supports de transmission est déjà commodément fournie, complétée de toutes les lois structurelles et dynamiques nécessaires pour les faire fonctionner ensemble. De plus, la structure de données spécifiée dans ce modèle se rapporte à la structure réelle des informations, de la même manière que la logique propositionnelle se rapporte à la logique dans son ensemble, incluant le calcul des prédicats et la théorie des modèles. En d’autres termes, un seul niveau de structure et de fonctionnalité est considéré, et l’attribution est principalement limitée à une paire de prédicats centraux communs aux deux théories, Vrai / Faux = 1 / 0. De même que la logique propositionnelle ne concerne que les relations fonctionnelles des variables propositionnelles et ignore leur contenu, la théorie de l’information ne s’intéresse qu’aux probabilités des symboles dans les chaînes de messages et ignore les détails de la structure syntactique et sémantique et du traitement.

Diagramme 12 : La logique propositionnelle et la théorie de l’information ignorent toutes deux des niveaux entiers de structure afin de réduire l’univers à des 1 et des 0. En logique propositionnelle, les variables propositionnelles sont uniquement distinguées par le fait qu’elles soient vraies ou fausses (1 ou 0), tandis que la théorie standard de l’information, ainsi que les théories de la calculabilité et de la cybernétique, traite des « données brutes » exprimées ou « codées » dans les termes les plus élémentaires possibles, à savoir les chiffres binaires 1 et 0. Alors que le rôle de ces « bits » est de réduire les incertitudes concernant des éléments de contenu spécifiques, certains détails essentiels de la structure syntactique et sémantique et du traitement, et des relations plus spécifiques entre les variables et les données, sont commodément omises. Les points d’interrogation rouges indiquent que ni la logique propositionnelle ni la théorie de l’information ne s’expliquent pleinement, ni leur modèle, ni leur support. [Diagramme partiellement adapté de Shannon, C.E.(1948), « A Mathematical Theory of communication », Bell System Technical Journal, vol.27, p.379-423 et 623-656.]

Cependant, la partie la plus intéressante de l’analogie est son extension logique. De même que la logique propositionnelle est naturellement étendue pour englober les niveaux d’attribution associés à la logique des prédicats et à la théorie des modèles, la théorie de l’information peut naturellement être étendue à des niveaux plus profonds d’attribution… En fait, les deux mêmes niveaux jouxtent la logique propositionnelle.

Le réoutillage du concept d’information comprend trois étapes. Premièrement, il doit être équipé des moyens de son propre traitement de transduction ou de transformation. Lorsque la transduction de l’information est reconnue (cognitivement) comme cognition généralisée, cela revient à la remplacer par un quantum de réflexivité à deux aspects, l’infocognition, qui incorpore la rétroaction télique. Deuxièmement, sa structure de bit, un mélange simpliste et plutôt sans inspiration de logique propositionnelle à deux valeurs et de théorie des probabilités, doit être étendue pour prendre en compte la logique dans son ensemble, y compris (1) la logique des prédicats, (2) la théorie des modèles et (3) la théorie du langage, incluant largement les théories des langages mathématiques, des métalangages et des grammaires génératives. Après tout, l’information n’attribuant que des prédicats organisés sur le plan linguistique à des objets dans le contexte de modèles, sa signification implique les mathématiques des prédicats, des langages et des modèles. Et troisièmement, elle doit être généralisée à un support ancestral ultime, la télèse, à partir duquel la syntaxe cognitive et son contenu informationnel survient par une rétroaction spécifiante en tant que partie d’un complexe unifié… un couplage récursif d’information et de méta-information, ou syntaxe transductive.

Ce réoutillage est réalisé en associant des informations à des opérateurs syntactiques réflexifs (unités d’infocognition cohérente) dans une structure linguistique réflexive, le Self-Configuring Self-Processing Language (SCSPL) [NDT : Langage Auto-Configurant Auto-Traitant], qui intègre son propre modèle et est donc identique à son univers. Le SCSPL évolue par conspansion (contraction matérielle qua expansion spatiale), une alternance grammaticale structurée entre une phase de « sortie » linguistique (réalité classique) constituée des états observables ou relations externes d’opérateurs syntactiques, et une « phase de production » qui transforme un état en un autre.

Ceci étant dit, il existe un sens dans lequel le monisme infocognitif est bien d’accord avec la thèse selon laquelle les bits sont des descripteurs universels de la réalité : comme les valeurs de bits 1 et 0 sont analogues aux valeurs de vérité de la logique à 2 valeurs, décrit par la logique à 2 valeurs implique qu’il peut être décrit en termes de bits. Cependant, si la réalité au sens large est définie par sa pertinence par rapport à la réalité perceptuelle au sens relativiste, elle ne consiste pas uniquement en une réalité perceptuelle seule.

La Réductibilité Télique et la Récursion Télique

La récursion télique est un processus fondamental qui tend à maximiser un paramètre d’auto-sélection cosmique, une fonctionnalité généralisée, sur un ensemble de relations syntaxe-état possibles à la lumière de la liberté d’auto-configuration de l’univers. Processus intrinsèquement « quantique » reflétant la place de la théorie quantique dans le SCSPL, la récursion télique est une forme de récursion « pré-informationnelle » associant une combinaison d’hologie, de rétroaction télique et de sélection récursive agissant sur le potentiel informationnel de MU, une forme primitive syndifféonique qui est symétrique par rapport au confinement.

Là où la réalité perceptuelle consiste en une infocognition (information auto-transductrice), expliquer la genèse et l’évolution de la réalité revient à expliquer la genèse et l’évolution de l’infocognition. Parce que la cognition généralisée (traitement de l’information) est temporelle, alors que l’information localise des objets ou des unités de message dans des espaces d’attribution, l’information et la cognition sont respectivement de nature spatiale et temporelle; L’infocognition est analogue à l’espace-temps et l’espace-temps est infocognitif. Il s’ensuit que la réalité perceptuelle ne consiste pas simplement en une infocognition mais en un espace-temps, et que chercher une explication de la genèse et de l’évolution de la réalité revient à chercher une explication de la genèse et de l’évolution de l’espace-temps qua infocognition… c’est-à-dire à la cosmologie dans le contexte d’une transduction d’information.

La cosmologie, grande tentative de l’humanité pour expliquer l’origine et la nature de l’univers, revient traditionnellement à rechercher un ensemble de « lois ultimes » capables d’expliquer non seulement comment l’univers fonctionne couramment, mais aussi comment il est arrivé là. Malheureusement, même si un tel ensemble de lois était trouvé, l’explication associée ne pourrait pas être considérée comme adéquate jusqu’à ce que les lois elles-mêmes soient expliquées, ainsi que les objets et attributs fondamentaux sur lesquels elles agissent. Cela soulève une question qui semble impondérable : comment expliquer un ensemble de lois, d’objets et d’attributs sans invoquer un autre ensemble de lois sous la forme d’une syntaxe explicative qui exigerait elle-même une explication, et ainsi de suite ad infinitum ?

La réponse se cache dans la question. Les lois ne tiennent pas toutes seules, mais doivent être définies par rapport aux objets et attributs sur lesquels elles agissent et qu’elles acceptent comme paramètres. Similairement, les objets et les attributs ne tiennent pas tous seuls, mais doivent être définis par rapport aux règles de structure, d’organisation et de transformation qui les régissent. Il s’ensuit que le support actif de la définition croisée possède la primauté logique sur les lois et les arguments, et est donc de nature pré-informationnelle et pré-nomologique… c’est-à-dire, télique. La télèse, que l’on peut qualifier de « potentiel infocognitif », est le support actif primordial à partir duquel les lois, leurs arguments et leurs paramètres émergent par raffinement mutuel ou récursion télique.

En d’autres termes, la télèse est une sorte de « pré-espace-temps » à partir duquel le temps et l’espace, la cognition et l’information, la syntaxe de transition d’état et l’état, n’ont pas encore émergé séparément. Une fois liées sous une forme infocognitive primitive qui dirige l’émergence en générant un « stress soulageable » entre ses composantes spatiales et temporelles généralisées, c’est-à-dire entre l’état et la syntaxe de transition d’état, la télèse continue à s’affiner en de nouvelles configurations infocognitives, c’est-à-dire de nouveaux arrangements de syntaxe de transition d’état, afin de réduire le stress entre syntaxe et état par le biais de la récursion télique (ce qu’elle ne peut jamais faire complètement, en raison des contingences résultantes inévitablement d’une récursion télique indépendante au niveau des parties de sous-systèmes localisés). En ce qui concerne la forme MU infocognitive primitive téliquo-récursive elle-même, elle n’« émerge » pas du tout, sauf de manière intrinsèque; elle n’a pas d’existence « externe » sauf comme l’une des myriades de possibilités qui existent naturellement dans un domaine illimité de contrainte zéro.

La récursion télique se déroule en deux étapes, primaire et secondaire (globale et locale). Dans l’étape primaire, des lois universelles (distribuées) se forment en juxtaposition avec la distribution initiale de la matière et de l’énergie, tandis que l’étape secondaire consiste en des transitions d’état matérielles et géométriques exprimées en termes d’étape primaire. C’est-à-dire que, lorsque les lois universelles sont syntactiques et que la distribution masse-énergie initiale correspond à l’état initial d’espace-temps, les transitions secondaires sont dérivées de l’état initial par des règles de syntaxe, incluant les lois de la physique, plus la récursion télique. La première étape est associée au téleur global, la réalité dans son ensemble; la seconde étape, avec des téleurs internes (observateurs-participants de « niveau agent »). Parce qu’il y a un sens dans lequel la récursion télique primaire et secondaire peut être considérée comme « simultanée », on peut dire que les téleurs locaux « créent l’univers » en y canalisant et en actualisant leur utilité généralisée à l’intérieur.

Diagramme 13 : Le diagramme ci-dessus illustre la relation entre la récursion télique primaire et secondaire, la dernière étant « incorporé dans » ou exprimée en fonction de la première. Les grands cercles et les flèches représentent les lois universelles (syntaxe distribuée) engagées dans la rétroaction télique avec l’état initial d’espace-temps (distribution initiale masse-énergie), tandis que les petits cercles et les flèches représentent la rétroaction télique entre les aspects contingents localisés de la syntaxe et de l’état via la conspansion. L’étape primaire maximise l’utilité généralisée globale sur une base ad hoc, tandis que les téleurs locaux maximisant librement et indépendamment leurs fonctions d’utilité locales. Les contreparties d’étape primaire de l’expansion interne et de la requantisation sont appelées coinversion et incoversion. C’est en vertu de la récursion télique que l’univers SCSPL peut être décrit comme son propre « protocalculateur quantique » auto-simulant et auto-actualisant.

Les modèles déterministes informatiques et de continuum de la réalité sont récursifs au sens standard; ils évoluent par des opérations d’état récurrentes à partir d’un ensemble fermé de « règles » ou de « lois ». Parce que les lois sont invariantes et agissent de manière déterministe sur un tableau discret statique ou continuum, il n’existe ni la place ni les moyens d’optimisation, ni aucune place pour l’auto-conception. Le CTMU, en revanche, est conspansif et téliquo-récursif; parce que de nouveaux potentiels d’états sont constamment créés par l’évacuation et l’absorption mutuelle d’objets cohérents (opérateurs syntactiques) à travers la conspansion, une incertitude métrique et nomologique prévaut chaque fois que la récursion standard est altérée par la rareté d’objets. Cela équivaut à une liberté auto-générative, fournissant hologiquement à la réalité un « bloc-notes auto-simulant » sur lequel comparer l’utilité agrégée de multiples auto-configurations à des fins d’auto-optimisation.

La récursion standard est « Markovienne » en ce que, lorsqu’une fonction récursive est exécutée, chaque récursion successive est appliquée au résultat de la précédente. La récursion télique est plus que markovienne; elle coordonne de manière auto-actualisante les événements à la lumière de relations d’ordre supérieur ou de télons qui sont invariants par rapport à l’identité globale, mais peut afficher un certain degré de polymorphisme sur les ordres inférieurs. Une fois que l’une de ces relations est nucléée par une opportunité de récursion télique, elle peut devenir un ingrédient de la syntaxe dans un ou plusieurs opérateurs téliquo-récursif (global ou niveau agent) ou téleurs et être « menée vers l’extérieur » par expansion interne, c’est-à-dire maintenu au sein de l’opérateur alors qu’il s’engage dans une absorption mutuelle avec d’autres opérateurs. Deux caractéristiques de l’espace-temps conspansif, l’homogénéité atemporelle des IED (strates d’opérateurs) et la possibilité d’une superposition étendue, permettent ensuite au télon de s’auto-actualiser « intelligemment », c’est-à-dire de manière téliquo-récursive, en coordonnant les événements de manière à engendrer sa propre émergence (soumise à diverses restrictions plus ou moins subtiles impliquant la liberté disponible, le bruit et les interférences concurrentielles d’autres télons). Dans tout système autonome et autodéterminant, la récursion télique fait partie intégrante des niveaux d’évolution cosmiques, téléo-biologiques et volitionnels41.

Le principe télique

Restreint au niveau d’explication téléologique (« Pourquoi? »), le MAP applique le Principe Télique : l’univers se configure en fonction de la nécessité de s’auto-sélectionner sur un fond de potentiel ontologique indifférencié ou télèse. Cette exigence, qui équivaut à un besoin de d’auto-actualisation et d’auto-expression, est implicite dans la forme MU. Le principe Télique est responsable de la conversion du potentiel en réalité de manière à maximiser un paramètre universel d’auto-sélection, l’utilité généralisée.

La téléologie, l’idée selon laquelle l’univers a un objectif qui explique son existence et guide son évolution, a commencé à perdre de l’importance devant la cour de l’opinion scientifique. Bien qu’il ait été d’abord assumé qu’une explication plus neutre, moins « théologique » à l’existence de l’homme et de l’univers viendrait combler le vide explicatif qui en résultait, il est finalement devenu évident qu’aucun remplacement de ce type ne tombait commodément des équations; une certaine interprétation de haut niveau serait nécessaire dans tous les cas. Cela a marqué l’essor du prétendu Principe Anthropique, qui se décline désormais en plusieurs versions, notamment « faible », « fort », « final » et celle privilégiée par Wheeler, « participative ».

La version initiale (faible), le Principe Anthropique Faible ou WAP [NDT : Weak Anthropic Principle], commence par le point trivial mais quelque part bayésien selon lequel nos observations cosmologiques de l’univers révèlent une capacité à la vie « parce que » l’univers porteur de vie est le seul type d’univers dans lequel il y a des êtres vivants capables de faire des observations cosmologiques. Cependant, alors que cela semble impliquer qu’il existe un domaine de nombreux univers dans lequel un tel univers peut être distingué passivement par la contrainte circonstancielle qu’il contienne des observateurs vivants, le WAP ne fournit aucune explication prête pour un tel domaine. En effet, pour ceux qui ne sont pas convaincus de ses vertus, le WAP semble presque ajouter une dose non nécessaire d’encre rouge explicative au registre cosmologique.

Le Principe Anthropique Fort (SAP) [NDT : Strong Anthropic Principle] élimine une grande partie de cette encre rouge en faisant une allégation plus extrême, affirmant que l’existence d’une vie intelligente n’est pas simplement un principe de sélection circonstanciel, mais une condition sine qua non de l’existence cosmique. En effet, cela limite l’ensemble des univers possibles à seulement ceux qui sont capables de produire la vie. Cependant, cela mène à des problèmes. Comment l’idée que les observateurs vivants sont nécessaires à l’existence de l’univers peut être conciliée avec l’idée que la réalité objective est essentiellement indépendante de l’observation et de ceux qui l’observent ? Et comment la vie intelligente, qui semble avoir évolué des milliards d’années après la naissance de l’univers, joue-t-elle un rôle causal quelconque dans la cosmologie ? Une sorte de « voyage dans le temps » se produit-il ? La sélection est une chose; l’auto-génération rétroactive en est une autre.

Il a souvent été soulevé que les principes anthropiques utilisent un raisonnement circulaire. C’est-à-dire qu’ils semblent prendre ce qu’ils prétendent expliquer, le fait observable que l’univers est « ajusté » pour supporter la vie, en tant que prémisse, affirmant que les êtres vivants observent que l’univers est amiable à la vie « parce que » la vie est présente dans l’univers pour faire cette observation. En d’autres termes, nous sommes ici pour observer l’univers, et l’univers est ici pour nous permettre de l’observer, car nous sommes ici pour observer l’univers ! Malheureusement, les principes anthropiques manquent de quelque chose dont ils auraient besoin pour que cela fonctionne : un modèle circulaire auquel leur raisonnement bouclé peut être constamment mis en correspondance. Tout simplement, le type de circularité causale qu’ils suggèrent est en porte-à-faux avec la « flèche du temps » et d’autres aspects des modèles non circulaires du temps et de l’espace prévalant.

Comme les arguments circulaires s’auto-justifient et résistent à la falsification, il est fréquemment supposé que la tautologie et le raisonnement circulaire sont des maux théoriques absolus. Mais c’est loin d’être le cas, car la logique et les mathématiques sont presque entièrement basées sur la circularité. Vérité et tautologie logique, récursion et itération, fermeture algébrique et topologique… tous l’entraînent dans une certaine mesure. Les problèmes ne se posent que lorsque le raisonnement circulaire est employé sans l’assurance d’une généralité mathématique complète, incorporant de fausses prétentions d’universalité sur des prémisses (qui peuvent être) non universelles.

Malheureusement, même les tautologies valides ne sont pas acceptées par l’école dominante de philosophie scientifique, le falsificationnisme. Alors que les tautologies non universelles sont à juste titre interdites en raison de leur résistance aux procédures falsificatives qui en révéleraient les limites, les tautologies universelles sont qualifiées de « scientifiquement sans intérêt « pour à peu près la même raison. Mais en réalité, la science ne pourrait exister d’aucune manière, forme ou façon sans elle. Cela soulève la possibilité que la pensée falsificationniste ait accidentellement occulté la véritable place du raisonnement tautologique dans la cosmologie.

Si l’univers est réellement assez circulaire pour supporter une forme d’argument « anthropique », sa circularité doit être définie et intégrée à sa structure de manière logique, et donc universelle et nécessaire. Le principe Télique affirme simplement que c’est le cas; L’impératif le plus fondamental de la réalité est de nature à lui imposer une structure supertautologique et conspansive. Ainsi, l’univers « se sélectionne » parmi les télèses non bornée ou UBT, un règne d’information zéro et de potentiel ontologique illimité, au moyen de la récursion télique, dans lequel la syntaxe infocognitive et son contenu informationnel sont croisés et raffinés à travers une rétroaction télique (état-syntaxe) sur toute la gamme de relations syntaxe-état potentielles, allant jusqu’à tout l’espace-temps et la réalité en général.

Le Principe Télique diffère des principes anthropiques de plusieurs manières importantes. Premièrement, il s’accompagne de principes de soutien et de modèles qui montrent que l’univers possède le degré de circularité nécessaire, en particulier par rapport au temps. En particulier, le Principe de Superposition Étendue, une propriété de l’espace-temps conspansif qui relie de manière cohérente des événements largement séparés, permet à l’univers de « se rétrodicter » lui-même à travers une rétroaction inter-temporelle significative. De plus, afin de fonctionner comme principe de sélection, il génère un paramètre de sélection globale généralisé analogue à « l’auto-utilité », qu’il cherche ensuite à maximiser à la lumière de la liberté évolutive du cosmos telle qu’exprimée par des sous-systèmes téliques localisés reflétant le système global cherchant à maximiser l’utilité (locale). À cet égard, le Principe Télique est une extension ontologique des soi-disant « principes d’économie » comme ceux de Maupertuis et de Hamilton concernant la moindre action, remplaçant la moindre action par une déviation de l’utilité généralisée.

Conformément à sa portée téléologique évidente, le Principe Télique n’est pas dépourvu de ce que l’on pourrait appeler des ramifications théologiques. Par exemple, certaines propriétés du langage réflexif et autonome de la réalité, à savoir qu’il est auto-distribué syntactiquement, qu’il se lit de lui-même et qu’il s’auto-configure et s’auto-traite de manière cohérente, correspondent respectivement aux propriétés théologiques traditionnelles d’omniprésence, d’omniscience et d’omnipotence. Bien que le genre de théologie que cela implique ne nécessite ni ne soutienne l’intercession de tout être « surnaturel » extérieur à l’univers réel lui-même, il soutient l’existence d’un être supraphysique (l’opérateur-concepteur global SCSPL) capable d’amener plus de charge sur des contextes physiques localisés que ce que peut voir l’œil ordinaire. Et parce que la partie physique (directement observable) de la réalité est logiquement insuffisante pour expliquer sa propre genèse, son maintien, son évolution ou sa consistance, elle est à elle seule incapable de contenir correctement l’être en question.

Un peu de contexte

Un examen de la théorie de la calculabilité classique du langage peut s’avérer utile. La théorie de la calculabilité reconnaît deux types généraux d’automates, les transducteurs et les accepteurs. Les transducteurs convertissent les entrées en sorties, tandis que les accepteurs classifient ou « reconnaissent » les entrées constituées de chaînes de symboles sans produire nécessairement de sortie.

Un transducteur fini est un 5-uplet (Σ, Q, Γ, δ, ω), où Σ est un alphabet d’entrée non vide fini, Q est un ensemble d’état non vide fini, Γ est un alphabet de sortie non vide fini, δ:Q × Σ R Q est la fonction de transition d’état et ω:Q × Σ R Γ est la fonction de sortie. À cela, nous pouvons ajouter un état de départ q0. Les transducteurs finis reposent ultimement sur des lois mécaniques pour fonctionner, transformant l’entrée informationnelle en sortie informationnelle en transformant leurs propres états.

Un accepteur fini est un 5-uplet (Q, Σ, δ, q0 , A), où Q est un ensemble fini non vide d’états internes, Σ est un alphabet, q0, est l’état de départ et A ⊆ Q est l’ensemble des états d’acception. La plage du mappage de transition δ détermine le type d’accepteur; il est déterministe si δ:Q×ΣR Q, et non déterministe si δ:Q×ΣR 2Q (où 2Q représente l’ensemble de puissance des états possibles). Un accepteur fini déterministe (Q, Σ, δ, q0 , A) accepte une chaîne x ∈ Σ * ssi δ (q0 ,x) ∈ A. Un langage est l’ensemble des chaînes acceptées par un automate ou une classe d’automates donnés.

Les langages sont générés par des grammaires. Dans la théorie de la calculabilité du langage, une grammaire générative (ou structure de phrase) G est un 4-uplet (N, T, P, σ) constitué de (1) un ensemble fini N de non terminaux; (2) un ensemble fini non vide T de terminaux, avec N∩T=∅ et N∪T = A (alphabet total de la grammaire); (3) un ensemble fini de productions P ⊂ ((N∪T)*\T*) × (N∪T)* constitué d’arguments non terminaux et de leurs transformations possiblement terminales; et (4) un élément σ de N appelé le symbole de départ. La mise en place d’une telle grammaire est un processus déductif allant du général au particulier; Partant du symbole le plus général σ (qui signifie « phrase »), des productions de plus en plus spécifiques conduisent à une configuration terminale. La production (x, y), souvent écrite xR y, signifie le remplacement de x par y ou, de manière équivalente, la substitution de y pour x. Où A* désigne l’ensemble de toutes les chaînes ou « mots » de A et A*\T* désigne le complément de T* de A*, un mot w∈(A*\T*) génère un autre mot w’ si w=w1 Xw2, w’=w1 X’w2, et XR X’ est une production.

La théorie des grammaires génératives les classe en fonction de l’accepteur le moins puissant pouvant reconnaître les langages qu’elles génèrent. Les grammaires de type 0 génèrent des langages illimités nécessitant un ordinateur universel (machine de Turing) avec une mémoire illimitée; les grammaires de type 1 génèrent des langages sensibles au contexte nécessitant un automate à bornes linéaires avec une mémoire proportionnelle à la longueur du mot; les grammaires de type 2 génèrent des langages sans contexte nécessitant un automate à pile avec une pile de mémoire dans laquelle un nombre fixe d’éléments est disponible en tout point; et les grammaires de type 3 génèrent des langages réguliers nécessitant un automate déterministe fini sans mémoire.

Il existe un parallèle évident entre les états et les transitions d’états des automates, et les chaînes et productions d’une grammaire. Un automate traite les chaînes d’entrée à travers ses états internes, en les exprimant en termes de son propre « langage interne ». En effet, un automate physique en train de traiter une chaîne d’entrée peut être vu comme une stratification linguistique dynamique intégrant le langage d’entrée, la programmation mutable de l’automate (incluant le code assembleur et machine), son architecture de câblage, le langage nomologique constitué des lois de la physique selon lesquelles le matériel fonctionne, et tout niveau de langage « métaphysique » nécessaire pour définir et maintenir les lois de la physique elles-mêmes. Étant donné que chaque langage de cette séquence est exprimé dans les termes de celui qui le suit, les langages forment un « imbrication descriptive » dans laquelle la syntaxe de chaque langue est distribuée sur toutes celles qui la précèdent.

La syntaxe d’un langage consiste en sa grammaire et la structure de ses expressions. C’est-à-dire qu’une syntaxe est une compilation des règles spatiales (structurelles) et temporelles (grammaticales, transformationnelles) du langage associé; ses règles sont invariantes, générales et distributives par rapport à l’ensemble des expressions composant le langage. Ce concept est aussi significatif pour les automates que pour les langages qu’ils traitent et s’applique à tous les niveaux de la stratification linguistique qui vient d’être décrite. Par exemple, lorsque le concept de covariance générale exprime la nature générale et distributive des lois de la physique, ces lois peuvent être considérées comme une « syntaxe « en soi, de même que les lois mathématiques plus générales s’appliquant aux diverses structures mathématiques auxquelles les lois de la physique se réfèrent implicitement.

La physique et les mathématiques ne sont généralement pas considérées comme des langages, mais comme des théories. Même s’ils sont nécessairement exprimés en termes de langage, ils sont généralement considérés comme « plus spécifiques ». Mais comme les automates, ils répondent aussi aux critères linguistiques. Par exemple, les théories mathématiques ont des syntaxes composées d’axiomes et de règles d’inférence, ainsi que diverses expressions dérivées telles que des définitions, des théorèmes et des corollaires. Plus généralement, une théorie est simplement une construction informationnelle jouant un rôle direct définitif, descriptif ou explicatif par rapport à quelque chose qui doit être défini, décrit ou expliqué. Parce que les théories consistent en chaînes identifiables de symboles prenant la forme d’énoncés et d’équations et obéissent à des « syntaxes » constituées d’axiomes, de principes, d’intuitions ou de règles empiriques, et partagent en fait leurs syntaxes avec les objets de la théorisation jusqu’à l’isomorphisme descriptif, elles sont des langages. En effet, les conditions mêmes de la théorisation, à savoir la perception et la cognition, sont des langages au sens où ils consistent en des « expressions » sensorielles ou conceptuelles et se conforment à des syntaxes logiques et non logiques consistant en des règles générales de structure et d’opération, incluant (mais pas nécessairement limité aux) les structures physiques et dynamiques de nos cerveaux et systèmes nerveux.

Passons rapidement en revue certains détails techniques des langages théoriques. Une théorie mathématique consiste en des propositions contenant des prédicats de base et des fonctions représentant des concepts fondamentaux. Par exemple, la théorie des ensembles est basée sur le concept d’appartenance (∈); la géométrie dépend fortement de concepts primitifs tels que l’angle et la distance; et l’arithmétique élémentaire intègre les concepts plus ou moins fondamentaux d’addition, de multiplication et d’ordre (<). Les symboles qui représentent ces concepts, parfois appelés constantes non logiques, constituent la signature Σ de la théorie. Cette signature comprend des symboles pour les relations, les fonctions et les individus, chacun avec une « arité » ou une valence. Au-delà de sa signature, une théorie mathématique contient des variables (symboles prédéfinis désignant des objets d’un domaine précédemment spécifié) pour des individus représentés par des symboles tels que (x, y, z,…), des symboles logiques (constantes logiques) tels que (~, ∧, ∨, →, ↔, =, ∃, ∀) et symboles techniques auxiliaires.42

Un langage élémentaire LΣ (langage du calcul des prédicats) peut être défini comme un ensemble d’expressions ou de formes propositionnelles incorporant ces symboles logiques et non logiques et leurs règles syntactiques. Les termes de LΣ sont définis comme suit : (1) les variables et constantes pour les individus sont des termes; (2) si F est un symbole de fonction n-aire et que t1, …, tn sont des termes, alors Ft1, …, tn est un terme; (3) une séquence de symboles est un terme si il est conforme à 1 et 2. Les expressions de LΣ sont caractérisées ainsi : (1) Où R est un symbole de relation n-aire et t1, …, tn sont des termes, Rt1, …, tn est une expression atomique (c’est-à-dire un cas d’attribution). (2) Si A et B sont des expressions, il en est de même de ~A, (A∧B), (A∨B), (A → B) et (A↔B). (3) Si A(x) est une expression contenant la variable x, mais pas ∃x ou ∀x, alors il en est de même de ∃xA(x) et ∀xA(x). (4) Une séquence de symboles est une expression uniquement si elle est formée conformément à 1-3. Par nature, les langages de la logique des prédicats sont descriptifs; leurs expressions décrivent des relations existant au sein de diverses structures mathématiques.43

Il convient maintenant de préciser que, pour définir un langage théorique, il faut simplement créer une syntaxe pour lui en étendant la syntaxe de la logique afin de prendre en compte les relations spatiales et temporelles nécessairement présentes dans ses constantes non logiques dans toutes les circonstances logiques (ou du moins la plupart) à l’intérieur du cadre prévu de la théorie. Comme la syntaxe de la logique elle-même, qui est une théorie de l’inclusion descriptive ou « vérité » fondée sur le besoin cognitif et perceptuel de distinguer ce qui est de ce qui n’est pas, la syntaxe d’un langage théorique repose également sur des ingrédients et des impératifs de réalité cognitive et perceptuelle. Nous avons déjà remarqué l’équivalence des automates et des langages; les états et les transitions d’état des automates sont parallèles aux chaînes et aux productions d’une grammaire. Pour trouver le langage théorique décrivant n’importe quelle classe de transducteurs, il suffit d’adjoindre à la syntaxe de la logique les descripteurs non logiques de leurs structures et processus transductifs.

Les scientifiques sont les principaux transducteurs du langage scientifique dans son ensemble, et leur syntaxe transductive comprend la syntaxe de l’observation scientifique généralisée et de la théorisation, c’est-à-dire la perception et la cognition. Nous pouvons donc partitionner ou stratifier cette syntaxe en fonction de la nature des éléments logiques et non logiques incorporés dans les règles syntactiques. Par exemple, nous pourrions développer quatre classes correspondant au trio fondamental espace, temps et objet, une classe contenant les règles de la logique et des mathématiques, une classe constituée du qualia perceptuel en fonction duquel nous définissons et extrayons expérience, sens et utilité de la réalité perceptuelle et cognitive, et une classe représentant des sentiments et des émotions plus nébuleux faisant partie intégrante de la détermination de l’utilité pour les relations qualiques.44 Pour le moment, nous pourrions aussi bien appeler ces classes SETO, SLM, SQP et SET, désignant respectivement la syntaxe espace-temps-objet, la syntaxe logico-mathématique, la syntaxe qualio-perceptuelle et la syntaxe emo-telic, ainsi qu’une relation de haut niveau entre ces composants et la structure à laquelle tous ou certains contribuent ultimement. Ensemble, ces ingrédients constituent la syntaxe Cognitive-Perceptuelle Humaine ou SCH.45

Comme chaque utilisateur de langage le sait, le traitement linguistique ne se limite pas à la reconnaissance et à la transduction. Il y a aussi la communication. Les concepts de langage et de communication sont indissociables; les langages sont des structures abstraites par lesquelles la communication est effectuée et la communication implique l’échange d’entrées et de sorties par les utilisateurs d’un langage. Chaque fois que nous avons une syntaxe, un ensemble d’expressions représentatives s’y conformant et un ensemble de processeurs de langage, nous disposons d’un langage et de la possibilité d’une communication significative entre ses processeurs. Lorsque la communication véhicule de l’information et que l’information représente des relations, la communication ne se limite pas aux états des communicateurs; il peut contenir toute information représentant tout type de relation. En conséquence, les communicateurs non seulement acceptent et transductent le langage, mais l’utilisent pour se représenter mutuellement leur vision du monde.

Le paradigme de la communication est parfaitement général et s’applique à toutes les échelles. Cela s’applique non seulement au niveau des expressions échangées par les communicateurs, mais également au niveau des informations d’état de base échangées par les éléments de traitement interactifs d’un automate. En d’autres termes, le traitement du langage lui-même peut être considéré comme une forme de communication; pour pouvoir actualiser un langage à travers une forme de traitement, celle-ci doit être intersectée avec un système de traitement fonctionnant par communication opérationnelle entre ses parties. Une machine universelle, par exemple, est un « système d’auto-communication » relayant des informations entre ses composants abstraits (en effet, la communication est l’incarnation même des trois opérations de base d’un ordinateur universel; à savoir la lecture, l’écriture et la relocalisation). Les règles structurelles et dynamiques des processeurs de langage correspondent donc directement aux syntaxes des langages; les deux types de système évoluent par intersection communicative de la syntaxe et de l’état (ou contenu). Il s’ensuit que les langages et les automates peuvent être traités sur un pied d’égalité et que, comme les automates peuvent être traités comme des systèmes d’auto-communication, il en va de même des langages.

Dans les descriptions techniques des automates et des langages décrits ci-dessus, un certain modèle du monde est implicite. Les automates acceptent les entrées du monde extérieur, les transforment en fonction de leurs états internes et renvoient (parfois) le résultat au monde extérieur quand elles ont terminé. Le langage et les informations se trouvent soit à l’intérieur soit à l’extérieur des automates, et elles ne sont à l’intérieur qu’une partie du temps. Le reste du temps, l’information est présumée traînant quelque part autour dans l’environnement ou en chemin d’un endroit à un autre. Mais là où la communication survient à toutes les échelles, la distinction entre intérieur et extérieur n’est pas si claire. Les langages communiqués entre les utilisateurs et les processeurs du langage, et les langages incarnés par les utilisateurs et les processeurs eux-mêmes, occupent un support global avec une syntaxe communicante unifiée largement indifférente à la distinction.

Les lois qui gouvernent un système peuvent être placées dans un espace qui contient ses objets ou dans les objets eux-mêmes. La physique classique appuie tout sur l’espace, en appliquant des concepts spatiaux tels que les vecteurs et les tenseurs à des champs extérieurs aux objets. Cependant, il est possible d’appliquer une transformation logique qui inverse cette image en la transformant en « extérieur-intérieur ». Cela aboutit à une « subjectivisation distribuée » dans laquelle tout se passe à l’intérieur des objets; les objets sont simplement définis pour intérioriser de manière consistante leurs interactions, plaçant ainsi chaque objet « à l’intérieur » de tous les autres de manière généralisée, plaçant ainsi les contenus de l’espace sur le même pied que celui précédemment occupé par l’espace contenant lui-même. Les vecteurs et les tenseurs deviennent alors des descripteurs des propriétés syntactiques internes et des états des objets. En effet, l’univers devient une « auto-simulation » fonctionnant à l’intérieur de son propre contenu.

Cette vue, qui est complémentaire à celle de la géométrique conventionnelle, est appelée algèbre transductive. La « double » relation entre la géométrie et l’algèbre transductive s’appelle la dualité conspansive. En conjonction avec d’autres principes, incluant l’hologie et la réductibilité infocognitive-télique-SCSPL, la dualité conspansive peut offrir une nouvelle vision de la nature de la réalité et du monde physique. On prend simplement l’image conventionnelle, la retourne à l’intérieur, assemble les deux images et en extrait les implications. La relation entre cette nouvelle image et l’ancienne est extensionnelle plutôt que concurrentielle, intégrant le modèle géométrique dans un modèle conspansif plus vaste et plus complet qui l’unit avec son modèle double. Dans tous les cas, tous les modèles équivalents sont sur un pied d’égalité et les seules hypothèses scientifiques sur lesquelles cette extension pourrait être mise en doute sont celles qui reposent sur l’hypothèse fallacieuse selon laquelle le modèle géométrique est « le gros de l’histoire ».

Introduction au SCSPL

Selon le Principe de Réalité, l’univers est autonome et, selon le monisme infocognitif, il régresse vers un royaume de contrainte nulle (télèse non bornée ou UBT) à partir duquel il doit s’affiner lui-même. Selon le Principe Télique, qui stipule que l’univers doit se produire lui-même avec les moyens de le faire, il doit faire et réaliser son propre « choix d’exister »; en raison de sa priorité absolue, cet acte de choix est identique à celui qui a été choisi, c’est-à-dire à l’univers lui-même, et donc réflexif. C’est-à-dire que « l’existence est partout le choix d’exister ». En conséquence, l’univers doit adopter une forme réflexive dans laquelle il peut se « sélectionner lui-même » pour une existence auto-définie, avec une fonction de sélection identique à celle sélectionnée. Cela signifie qu’il doit prendre une certaine forme générale ou « initiale », la forme MU, qui contient toutes les conditions requises pour générer le contenu de la réalité. En raison de l’hologie, selon laquelle l’univers autonome n’a rien d’autre que lui-même en quoi consister, cette forme est auto-distribuée.

On pourrait d’abord être tenté d’objecter qu’il n’y a aucune raison de penser que l’univers n’est pas simplement « existant », et donc que l’auto-sélection est inutile. Premièrement, il s’agit d’un appel plus ou moins subtil à quelque chose d’extérieur à l’univers, à savoir un moyen d’information antérieur/externe ou une « syntaxe » d’existence; si une telle syntaxe était suffisamment pertinente par rapport à cette réalité, c’est-à-dire suffisamment réelle pour soutenir son existence, elle serait alors analytiquement incluse dans la réalité (telle que définie jusqu’à la pertinence perceptuelle). Deuxièmement, l’auto-sélection active est en effet nécessaire, car l’existence n’est pas simplement un état mais un processus; l’univers doit distinguer intérieurement ce qu’il est de ce qu’il n’est pas, et la passivité est exclue car elle impliquerait à nouveau la participation d’un principe actif complémentaire d’origine extérieure.

Selon le Principe de la Réductibilité Linguistique, la réalité est un langage. Parce qu’il est autonome en ce qui concerne le traitement ainsi que la configuration, il s’agit d’un Langage Auto-configurant Auto-Traitant [NDT : Self-Configuring Self-Processing Language] ou SCSPL, dont la structure spatio-temporelle générale est reproduite hologiquement partout au dedans en tant que syntaxe auto-transductive. Cela réduit la phase générative de la réalité, y compris la cosmogonie physique, à la grammaire générative du SCSPL. Cette grammaire génératrice de réalité s’appelle grammaireΓ, et la forme MU, étant la forme de réalité la plus générale ou la plus antérieure, en est la base. Selon le Principe du Monisme Infocognitif et de l’hologie de MU, le SCSPL consiste en une infocognition configurée par MU, et la grammaire Γ décrit la génération et la transformation de ce constituant universel.

Le SCSPL n’est pas un langage ordinaire et la grammaire Γ n’est pas une grammaire générative ordinaire. Les raisons viennent des limites inhérentes à la théorie des langages calculatoires. Dans la théorie calculatoire standard, un langage est constitué de l’ensemble des chaînes acceptées par un automate ou une classe d’automates donné; Par exemple, un langage L est appelé « normal » s’il y a un automate à états finis qui l’accepte. Cependant, cette approche est inadéquate pour le SCSPL. Premièrement, elle est centrée sur le calcul, un type général de traitement de l’information associé à un automate abstrait, la machine de Turing ou « ordinateur universel », qui n’aurait jamais pu générer la structure informationnelle de l’univers réel. En tant que construction informationnelle et méta-informationnelle (syntactique), l’ordinateur universel peut lui-même rendre compte de la genèse de la syntaxe ou de l’information. Deuxièmement, contrairement aux langages ordinaires, le langage de la réalité ne peut pas s’appuyer sur un esprit externe, un automate ou un substrat matériel préexistant pour la reconnaissance et le traitement. Étant donné que tout processeur suffisamment réel pour reconnaître et traiter la réalité fait nécessairement partie de la réalité, la distinction langage-processeur est sans force ontologique.

Ainsi, alors que les modèles de réalité discrets ordinaires reposent largement sur la distinction langage-processeur, le SCSPL n’a aucune dette de la sorte. Par exemple, les modèles d’automates cellulaires distinguent généralement un tableau spatial, les objets informationnels existant dans ce tableau et l’ensemble distribué de règles de transition d’états temporels par lesquelles le tableau et son contenu sont régulés. En revanche, le SCSPL considère le langage et le processeur comme des aspects d’une unité infocognitive sous-jacente. Par une dualité conspansive (ectomorphisme-endomorphisme), les objets SCSPL contiennent l’espace et le temps au sens aussi réel que celui où l’espace-temps contient les objets, entraînant une identification partielle de l’espace, du temps et de la matière. Le SCSPL est plus qu’un langage de programmation réflexif doté de la capacité d’auto-exécution calculatoire; c’est une entité protocalculatoire capable de récursion télique et ainsi, de générer sa propre structure et dynamique informationnelle et syntactique.

Alors que les modèles calculatoires ordinaires ont un caractère informationnel et syntactique, la nature protocalculatoire du SCSPL nécessite une généralisation des informations et de la syntaxe. En ce qui concerne l’origine ou la nature ultime de la réalité perceptuelle, l’explication est un processus réductif/inductif qui délie de manière régressive les contraintes afin de mettre au jour celles de la plus haute priorité et généralité. Ce processus aboutit finalement au descripteur intelligible le plus fondamental qui puisse être formulé, au-delà duquel ne se trouve que l’inintelligible. Cela marque la transition de l’information et de la syntaxe vers une généralisation réductrice convergente, la télèse.46

Cela pointe vers une propriété universelle du langage : il est dynamique. Bien que l’on suppose souvent commodément que les langages sont des idéaux Platoniciens intemporels qui attendent d’être traitées par des accepteurs externes, ils ne peuvent être traités en termes d’informations statiques que par les utilisateurs ou les processeurs qui leur fournissent une syntaxe transductive externe, et seulement ensuite en négligeant certaines nécessités sous-jacentes. Par exemple, pour réaliser physiquement la structure informationnelle d’un langage sur un support imprimé ou électronique, celui-ci doit être exprimé en termes de particules physiques qui reconnaissent dynamiquement leurs localisations mutuelles dans la mesure nécessaire pour maintenir les relations spatiales constituant sa structure informationnelle. C’est une exigence générale, qui va du physique et concret au mathématique et abstrait.

Ainsi, les langages sont finalement auto-traitants; ils doivent soit contenir leurs processeurs dans leurs expressions, soit être exprimés en termes de langage plus élémentaire répondant à cette exigence. En conséquence, les expressions du SCSPL sont des configurations informationnelles dynamiques de processeurs d’information, ce qui implique que le SCSPL est partout constitué d’informations et d’une syntaxe acceptive-transductive dans un état d’intersection logique. Ensemble, l’information et la syntaxe comprennent l’infocognition, auto-transduction de l’information sous la forme d’opérateurs syntactiques SCSPL qui « communiquent » de manière croisée-absorbante en acquérant les états informationnels les uns des autres en tant que contenu cognitif-syntactique. C’est à la base commune de ces deux composants que les informations peuvent être réduites dans le contexte SCSPL. Lorsque le terme télèse désigne cette composante commune d’informations et de syntaxe, la grammaire SCSPL affine l’infocognition en liant ou en contraignant la télèse comme infocognition.

Dans la mesure où une grammaire fonctionne par l’application récursive de règles syntactiques, la grammaire SCSPL est récursive (« auto-appelante »). Cependant, la grammaire SCSPL n’est pas simplement récursive de manière déterministe ou non déterministe, elle est également téliquo-récursive. Alors qu’une grammaire ordinaire traite de manière récursive des informations ou lie un potentiel informationnel à une syntaxe invariante distribuée sur ses produits, la grammaire Γ lie la télèse, potentiel infocognitif couvrant des relations possibles entre syntaxe et état, en croisant-raffinant la syntaxe et son contenu informationnel par récursion télique. La récursion Télique est le processus responsable de la configuration des relations syntaxe-contenu sur lesquelles est basée la récursion informationnelle standard; son existence est une exigence ontologique de la réalité. Le raffinement croisé téliquo-récursif de la syntaxe et du contenu est implicite dans la « graine » de la grammaire Γ, la forme MU, qui intègre le potentiel de complémentarité parfaite entre la syntaxe et l’état, la loi et la matière.

Etant donné que ce potentiel ne peut être spécifiquement réalisé que par la liaison infocognitive de la télèse et que la liaison télique localisée est effectuée librement et indépendamment par des opérateurs téliques localisés mutuellement décohérents, les déviations par rapport à la complémentarité parfaite sont omniprésentes. L’évolution SCSPL, qui peut être considérée comme une tentative d’aider cette complémentarité à émerger de son statut potentiel dans MU, incorpore un invariant global (syntactique) qui travaille à minimiser la déviation totale de la complémentarité parfaite de la syntaxe et de l’état en tant qu’opérateurs syntactiques liant librement et indépendamment la télèse. Cet invariant SCSPL principal, le Principe Télique, prend la forme d’une fonction de sélection avec un paramètre quantitatif, l’utilité généralisée, liée à la déviation. Le Principe Télique peut être considéré comme l’élément principal de la syntaxe SCSPL… le « choix d’exister » auto-sélectif distribué dans l’espace-temps coïncidant avec MU.

Le SCSPL incorpore les concepts de stratification syntactique et de distribution syntactique. Par exemple, comme les lois des mathématiques s’appliquent partout en raison des lois de la physique, ces premières se distribuent sur les dernières au sens syntactique. Ainsi, lorsque les lois des mathématiques et de la physique sont désignées par S1=SLM et S2 respectivement, S1 se distribue sur S2, c’est-à-dire forme un revêtement syntactique pour S2. Cela signifie essentiellement que les lois mathématiques sont partout une composante syntactique requise du langage de la physique. À S2 est associé un « sous-langage » SCSPL appelé LO (avec une lettre O en indice). LO constitue le monde de la perception, l’univers objectif classique des données sensorielles traditionnellement étudiées par la science. LO est contenu dans la phase téliquo-récursive pré-informationnelle du SCSPL, LS, qui englobe le raffinement croisé de la syntaxe LO et du contenu LO de l’aspect pré-infocognitif du SCSPL. La partie de la grammaire SCSPL confinée à LO incorpore certaines restrictions auxquelles LS n’est pas soumis; Par exemple, la partie grammaticale de LO (S2) est fixe, distribuée et supposée continue, alors que celle de LS peut également être modifiable, locale et discrète… en un mot, télique.

La grammaire Γ est la grammaire générative du SCSPL = (LS ⊃ LO). La grammaire Γ ne ressemble pas à une grammaire ordinaire en ce que ses processeurs, produits et productions coïncident et se forment mutuellement par récursion télique. La syntaxe et l’état, vaguement analogues à la forme et au contenu (ou aux productions et aux produits), s’affinent mutuellement, de la télèse à la récursion télique par des processeurs infocognitifs. Les règles de production incluent le Principe Télique, des éléments de syntaxe distribués formés au cours de la phase principale de la récursion télique, et des télons plus ou moins polymorphes formés par des téleurs de niveau agent. Les modes de production correspondants sont la récursion télique globale, la récursion informationnelle par syntaxe distribuée et la récursion télique locale.

Les « mots » produits par la grammaire Γ ne sont pas des chaînes de symboles, mais des relations spatiales LO parmi des processeurs parallèles capables de lire et d’écrire dans leurs états respectifs. En effet, les états de ses processeurs sont à peu près analogues aux symboles et aux chaînes d’un langage ordinaire. Les processeurs de la grammaire Γ fonctionnent donc non seulement comme des transducteurs, mais également comme des emplacements symboliques pour les observables et les valeurs, tandis que leurs états externes correspondent à des produits et que leurs transitions d’état réalisent les productions de la grammaire. En d’autres termes, les états et les transitions d’état des processeurs de la grammaire Γ comprennent une représentation de la grammaire Γ, présentant le SCSPL comme un langage dynamique auto-modélisant ou « auto-simulation interactive ».

Dans la description suivante, les produits sont limités aux produits finaux physiques associés à LO. Cela ne doit pas être interprété comme signifiant que seuls les produits SCSPL sont des produits physiques; En fait, tout dans le SCSPL est dans une certaine mesure un « produit » téliquo-récursif de tout le reste. Cependant, lorsque l’explandandum principal est la réalité physique (observable scientifiquement), LO constitue un choix approprié.

Γ = (O, R, P, μ) contient

(1) Un ensemble O d’objets réflexifs actifs comprenant Γ lui-même, les transformateurs (producteurs-réducteurs) 47 de Γ. Tous les processeurs sont capables de, et réactif à la, récursion informationnelle (déterministe). O inclut un ensemble distingué Σ = {Γ, A, Q} d’opérateurs syntactiques, processeurs cohérents capables de, ou sensibles à la, récursion télique. En général, les parties de la syntaxe SCSPL actives au sein d’un opérateur donné dépendent de son type spécifique. Σ inclut le processeur global Γ, l’ensemble Q = {qi } de particules stables réductibles et irréductibles réactives à la récursion télique à un degré proportionnel à leur liberté et à leur cohérence, ainsi que l’ensemble A d’agents téliques, opérateurs téliquo-récursifs actifs, ou téleurs capables d’exprimer la téléologie au niveau local. Les éléments de A ne doivent pas nécessairement occuper LO, mais peuvent exister dans LS. Où υ désigne le paramètre d’auto-sélection généralisé de Γ, les éléments de A sont requis par Γ en tant que « contrôleurs de capteurs » internes υ-réactifs.

(2) Un ensemble R = (RO , RS) de produits contenant un sous-ensemble RO = (σO , τO , πO) d’états de produits LO incluant toutes les relations de LO, et un sous-ensemble RS de télons ou « pré-produits » générée dans LS par récursion télique associée à des opérateurs syntactiques globaux ou de niveau agent. Les éléments de σO sont des relations spatiales, ceux de τO sont des relations temporelles et ceux de πO sont des relations spatiotemporelles contenant à la fois des relations σO et τO. σO est constitué de relations d’états pour lesquelles les transducteurs correspondants n’ont pas d’entrée réciproque; τO est constitué de séquences d’états consécutifs d’objets uniques; et πO est constitué de processus ou de combinaisons des deux. En général, ces états ne sont pas entièrement déterminés par la transformation des règles d’état LO, mais nécessitent une augmentation télique pour leur actualisation.

(3) Un ensemble P = (N, T) constitué des productions de Γ. N est constitué des descripteurs distribués de πO, incluant les descripteurs markoviens distribués spatiotemporellements et conservateurs appelés « lois de la physique », tandis que T consiste en des entités LS actives analogues à celles de N mais associées à des télons spécifiques (pré-produits) de RS et sujet à des variations locales coordonnées dans le contexte des relations téloniques d’ordre supérieur. Les éléments de N sont déterminés à l’étape primaire de la récursion télique, tandis que ceux de T sont déterminés au stade secondaire de la récursion télique.

(4) Une configuration de départ, la forme MU μ, qui est identique à l’événement de récursion télique qui la crée (la création du SCSPL et de la grammaire Γ est une récursion télique, pas une récursion informationnelle-algorithmique). C’est cette identité d’événement et de résultat qui détermine les caractéristiques spatiales et temporelles innées de l’espace-temps, pour laquelle µ est la « graine ». La forme MU peut être considérée comme une « perturbation intrinsèque » ou une « asymétrie intrinsèque » en UBT. La forme MU est distribuée sur le SCSPL.

Un processeur d’une grammaire G est un système dynamique naturel ou artificiel qui opère, change d’état ou traite des informations conformément aux règles de G. Contrairement aux grammaires génératives ordinaires, la grammaire Γ ne nécessite aucun processeur externe; ses processeurs et productions sont identiques. Ainsi, la grammaire Γ est exécutée par ses propres productions à des niveaux de distribution syntactique allant du niveau global au niveau objet. En fait, O, R et P – processeurs, produits (états) et événements de production – coïncident tous et présentent ainsi une forme de trialité. Cette coïncidence à trois voies est caractéristique de la grammaire Γ et reprend nombre de ses caractéristiques essentielles.

La coïncidence O-R-P est déjà, dans une certaine mesure, réalisée dans le modèle langage-grammaire-processeur standard de la théorie du calcul, mais seulement par inadvertance. Alors que le traitement linguistique est dynamiquement mis en parallèle par des modifications des états interne et externe des processeurs, ceux-ci sont toujours considérés comme distincts de la langue et de la grammaire en cours de traitement. De plus, le support de traitement de base n’est pas pris en compte, le modèle n’est pas autosuffisant et la récursion est purement informationnelle et calculatoire; il n’y a pas d’allocation pour l’infocognition ou la récursion télique. Le SCSPL ne partage aucune de ces limitations.

La grammaire Γ génère le SCSPL en fonction de l’utilité de ses processeurs sentients, y compris l’auto-utilité de Γ et l’utilité de ses relations LO avec les télors en A. Γ et A génèrent des télons respectivement aux niveaux global et local; ainsi, ils doivent être capables de reconnaître et de maximiser le paramètre de sélection υ (dans le cas de télors humains, par exemple, cela nécessite les composants SQP et SET du SCH). En tant que tels, ils sont responsables de la récursion télique et peuvent être considérés comme les « générateurs » de la grammaire Γ, alors que l’ensemble Q d’objets physiques élémentaires est acquis librement et compétitivement par les télons et occupe ainsi une position ontologique secondaire.

La Γ grammaire est conspansive. Les processeurs non globaux alternent entre la génération et l’actualisation sélective de productions possibles, et donc entre les phases génératives et sélectives (intérieures expansives et requantisatives) de la conspansion. La phase sélective d’un opérateur coïncide avec des événements interactifs d’acquisition mutuelle, tandis que la phase générative coïncide avec la génération et l’actualisation sélective de productions possibles par multiplexage hologique. En conjonction avec la superposition spatio-temporelle étendue, la conspansion fournit les moyens de la récursion locale (télique et informationnelle).

Son taux est donc un « facteur de conversion espace-temps » globalement invariant, et comme tous les changements d’état local doivent être exprimés en termes de celui-ci, il est maximal. Ce taux de production maximal invariant est appelé taux de conspansion c et peut être identifié physiquement à la vitesse de la lumière in vacuo.48 Les implications de la constance de c et de N à la lumière du MAP ont déjà été soulignées en ce qui concerne l’accélération de l’expansion d’apparence interne de l’opérateur global.

Il est instructif d’expérimenter les différentes constructions pouvant être placées sur LS et LO. Par exemple, on peut penser à LS en tant que « L-sim », reflétant son aspect auto-simulatif, téliquo-récursif, et à LO, en tant que « L-out », le résultat de cette auto-simulation. On peut associer LO aux états observables et à la syntaxe de transition d’état déterministe distribuée, et LS au Principe Télique métasyntactique. On peut même penser que LS et LO sont respectivement internes et (partiellement) externes aux opérateurs syntactiques SCSPL, et correspondent donc vaguement aux aspects subjectifs et objectifs de la réalité. Là où LS et LO sont associés à des phases d’expansion interne cohérente et de requantisation décohérente de la conspansion, il en est de même de la réalité subjective et objective, de la simulation et du résultat, « onde et particule ». En d’autres termes, la distinction subjectif-objectif, ainsi que la complémentarité, peuvent être considérées comme des fonctions de la dualité conspansive.

Le fait que LO ait une structure feuilletée composée de feuillets de type espace, avec des règles temporelles confinée aux opérateurs incorporés dans les feuillets, suggère que son niveau de structure inter-opérateur (organisée en état, ectosyntaxique) soit considéré comme de nature essentiellement spatiale. Ainsi, lorsque l’espace désigne les relations externes entre les opérateurs et que le temps indique leurs relations internes, on pourrait aussi penser que LS et LO correspondent approximativement à l’espace et au temps. (La correspondance est « approximative » car LS et LO sont mutuellement inclusives, reflétant le couplage logique espace-temps; LO contient topologiquement des opérateurs (LO, LS)-structurés, tandis que les opérateurs contiennent descriptivement LO.) Lorsque l’espace et le temps correspondent respectivement à l’information et à la combinaison de la cognition généralisée et de la récursion télique, on peut donc en conclure que l’évolution conspansive de l’espace-temps est une alternance de phases téléo-cognitives et informationnelles raffinées-croisées par une récursion télique impliquant des relations téloniques trans-markoviennes étendues.

Bien qu’il contienne l’aspect observable du SCSPL, LO peut en principe contenir des paramètres cachés (inobservables) impliqués dans des relations nomologiques et donc pertinents pour l’état physique. En d’autres termes, outre les variables dynamiques standards de la physique, LO peut contenir des variables dynamiques supplémentaires qui ne peuvent pas être observées directement, mais uniquement inférées théoriquement sur la base d’observations plus ou moins générales. Par exemple, les théoriciens des cordes, les théoriciens-M et autres spéculent souvent que l’univers pourrait flotter dans une sorte d’espace englobant externe, dont la relation donne une valeur explicative concernant l’état ou la condition interne de l’univers lui-même. La dualité conspansive SCSPL suggère que « l’externalité » putative d’un tel espace n’est pas une propriété significative; si un tel espace existe et est suffisamment pertinent pour l’univers dans lequel nous vivons pour avoir pour nous une valeur explicative, il est alors par définition un ingrédient de la syntaxe SCSPL et peut donc être considéré comme résidant dans les opérateurs syntactiques SCSPL. En fait, c’est une conséquence directe du Principe de Réalité.

Bien qu’il soit possible d’aller plus loin, le présent document a pour but de présenter un aperçu général de la théorie plutôt qu’un développement exhaustif. En conjonction avec les principes et caractéristiques énumérés ci-dessus, le cadre donné devrait suffire à caractériser le SCSPL sur une base introductive et à le distinguer en termes de variété et de contenu d’autres théories.

Le SCSPL comme Circuit Auto-Excité

Nous sommes maintenant en mesure d’établir quelques parallèles entre la vision de Wheeler de la théorie de la réalité et le CTMU.

Le Circuit Auto-Excité, la boucle logique informationnelle par laquelle la physique engendre la participation des observateurs, qui engendre l’information, qui engendre la physique, est une caractérisation étroite du SCSPL… si étroite qu’il serait difficile, voire impossible, de remplacer le SCSPL par quoi que ce soit et ne pas violer ni tomber en deçà de la description de Wheeler. Le SCSPL est logique dans sa construction, possède une dynamique bouclée, et crée information et syntaxe, y compris les lois de la physique, par le biais de la récursivité télique générée par des opérateurs syntactiques de niveau de agent, dont les actes de participation-observateur sont essentiels à la l’auto-configuration de l’Univers Participatif. Ces actes sont liés par récursion télique aux interactions cognitives-perceptuelles généralisées des opérateurs syntaxiques de niveau quantique, les événements minimaux comprenant la trame de l’espace-temps.

Grâce à la rétroaction télique, l’état et la syntaxe sont croisés-affinés à partir d’une télèse non bornée ou UBT, un domaine de potentiel ontologique d’information zéro, sous la direction d’une loi d’ordre supérieur appelée Principe de Télique… une « loi sans loi » protéique par laquelle l’ordre est extrait du désordre lorsque les lois sont configurées en fonction de l’utilité généralisée des relations état-syntaxe pour les opérateurs de niveau agent ou les observateurs-participants. Les indications binaires oui-ou-non prescrites par It from Bit sont demandées par le monisme infocognitif et par le statut fondamental de la logique propositionnelle à deux valeurs dans la syntaxe SCSPL. Le monde n’est pas simplement une monstruosité cybernétique, une « machine géante régie par une loi préétablie », mais un système métacybernétique avec une priorité logique sur les machines et les lois auxquelles elles obéissent.

Comment survient l’existence ? est répondu par le fait que l’univers est un opérateur SCSPL global qui équivaut à un vaste acte réflexif de participation-observateur réflexif, auto-sélectif et auto-expressif, tandis que comment survient le quantique ? est répondu par l’auto-réplication hologique de l’univers dans chacun de ses microscopiques opérateurs syntaxiques et téleurs de niveau agents. De nombreux observateurs-participants produisent un monde cohérent car, à travers MU, l’univers est associé à son contenu en tant que syntaxe distribuée homogène qui supporte et exprime syndifféoniquement leurs distinctions, même lorsqu’ils l’aident à évoluer grâce à l’observateur-participant et à la récursion télique. Le solipsisme individuel devient solipsisme distribué par l’absorption mutuelle des opérateurs syntactiques SCSPL, rendue possible par une combinaison de la syntaxe SCSPL distribuée et de la téléologie partagée.

Le Principe de Réalité, ainsi que le MAP, M=R et d’autres garants logiques de l’autonomie cosmique, montre que la stabilité syntactique de la réalité exclut toute régression infinie reptilienne de tortues sur tortues, alors que le continuum familier de la physique classique correspond à une interpolation syntactique (SLM) de la variété conspansive générée par les opérations grammaticales SCSPL discrètes. Lorsque l’espace et le temps correspondent respectivement à l’information et à la cognition généralisée, et lorsque l’information et la cognition sont logiquement liées dans des opérateurs syntaxiques SCSPL infocognitifs intersectés dans des états et des événements de transition d’état, l’espace et le temps sont entrelacés dans un réseau d’événements conspansif connecté par la syntaxe et évoluant par des événements d’absorption mutuelle entre opérateurs syntactiques, des instances symétriques d’observation généralisée influencées par la récursion télique. Ainsi, le temps n’est pas « introduit dans » l’explication de l’existence, mais est une fonction de la grammaire SCSPL téliquo-récursive conspansive.

La « limite de la limite » ultime de l’univers est l’UBT, un royaume de contrainte nulle et de possibilité infinie où ni limite ni contenu n’existent. L’univers supertautologiquement fermé achète des difféonèses internes uniquement au prix d’une synèse globale, n’achetant ses distinctions informationnelles qu’au prix de la cohérence. Aucune question, aucune réponse ne reflète le fait que la réalité ne consiste pas en une simple information, mais en une infocognition, et que l’information sur l’état est fondamentalement liée et dépendante de la syntaxe… la syntaxe des « questions » posées à elle-même par l’univers auto-configurant. En raison de la liberté d’auto-configuration héritée de l’UBT par la réalité, l’univers dynamiquement auto-configurant affiche incertitude et complémentarité et ne peut donc pas être verrouillé dans des réponses déterminées localement pour toutes les questions possibles à la fois, tandis que l’auto-connectivité étendue de l’espace-temps conspansif implique inévitablement l’environnement dans la Q&R.

Le Principe Super-Copernicien reflète la distribution de l’événement de création sur chaque point de l’espace-temps, conformément au principe de Superposition étendue, qui décrit la manière dont les états et événements consécutifs se superposent de manière atemporelle dans leurs états et événements antécédents. La Conscience Généralisée, la réflexivité unitaire de l’univers, est une description juste de l’auto-configuration et de la capacité d’auto-traitement du SCSPL telles que capturées par les principes Télique et M=R, tandis que l’espace-temps conspansif lie des objets distants spatialement et temporellement dans une toile de contact et de communication dépassant même la connectivité neurale d’un cerveau humain. Et le CTMU décrit l’univers comme étant simplement le type de système d’information complexe, téléologiquement auto-variant et auto-synthétisé prescrit par plus est différent, téliquo-récursivement expliquant la multiplicité et la difféonèse de l’unité et de la synèse de la syntaxe SCSPL distribuée, la contrepartie (unique) du CTMU de ce qu’on a parfois appelé « l’ordre implicite ».49

L’analogie ci-dessus n’est que partielle et il n’est nullement sous-entendu que la présentation actuelle est sans lacunes. Mais en toute justice, plusieurs points cruciaux peuvent être soulevés en faveur du CTMU, même à ce stade précoce de l’exposé. Premièrement, il est supertautologique; étant conçu pour refléter la tautologie logique jusqu’au niveau de la théorie des modèles et au-delà, il est vrai à peu près de la même manière qu’une théorie des mathématiques pures serait vraie, mais en référence à un univers élargi consistant à la fois en une réalité mathématique et une réalité physique. En effet, le CTMU peut être considérée comme une théorie de la structure mathématique d’un nouvel objet mathématique, le SCSPL. Deuxièmement, il a beaucoup plus de portée explicative que d’autres théories, fournissant un cadre capable d’adapter la logique de la cosmogonie autodéterminante sans exclure de manière préjudiciable (par exemple) les aspects subjectifs et non matériels de la réalité. Troisièmement, il intègre en grande partie les modèles actuels de réalité, au moins dans la mesure où ces modèles n’ont pas déjà été poussés au-delà de leurs capacités explicatives. Et quatrièmement, il a ce qui semble être des implications empiriquement valables absentes d’autres théories, sauf en tant qu’hypothèses ou observations inattendues, par ex. l’expansion cosmique en accélération. Mais peut-être que le plus important à ce stade est que, en principe, toute lacune explicative apparente puisse être comblée. C’est à dire, si quelque chose peut être expliqué dans le domaine de la science standard, il peut être encore mieux expliqué dans un modèle inclusif renforcé par la dualité conspansive.

Les ramifications du CTMU sont suffisamment étendues pour que leur émergence d’une théorie unique exige presque une explication à elle seule. Les implications scientifiques, mathématiques et philosophiques du CTMU sont nombreuses et variées, jouant une gamme allant de la physique fondamentale et de la cosmologie à la biologie de l’évolution, à la théorie de la cognition, aux fondements des mathématiques et aux philosophies du langage et de la conscience. Mais pour être juste, rien de moins n’est à attendre d’une véritable « théorie de la réalité », en particulier d’une qui prend la forme d’une description de la relation entre l’esprit et l’univers. Après tout, le CTMU est ainsi nommé car il s’agit d’une interprétation croisée symétrique de la réalité mentale et physique, qui transpose logiquement l’univers concret en une théorie abstraite de la cognition généralisée et inversement selon le Principe M=R. Si ses implications étaient moins profondes, il serait mal classé et mal nommé.

Le CTMU dit que la réalité est un langage… une structure auto-explicative, auto-théorisante, auto-modelante identique à son univers. En tant que tel, il peut être considéré comme une limite ou une « contraction » de la théorie des modèles dans laquelle théorie et univers coïncident au niveau syntactique de la structure théorique. Tandis que la plupart des théories scientifiques sont, avec optimisme, représentées dans ou sur l’univers à travers un gouffre dualiste infranchissable, le CTMU est une théorie monique de la perception qui élimine simplement le gouffre en injectant tautologiquement la logique dans son intégralité, y compris les extensions logiques de la théorie des modèles et la logique des théories formalisées, dans la réalité en tant que syntaxe distribuée auto-transductive. Le CTMU est capable de le faire car il est un fait mathématique évident que tout ce qui n’est pas conforme à la syntaxe de la logique est incohérent et ne fait donc pas partie d’une quelconque réalité stable et cohérente. Parce que la réalité que nous habitons est visiblement stable et cohérente, l’exactitude de ce geste est assurée. En éliminant le gouffre théorie-univers au niveau de la syntaxe cognitive et perceptuelle, le CTMU remplit admirablement le critère de l’économie théorique… et de façon supertautologique.

Le CTMU peut-il être considérée comme une réalisation de la vision de Wheeler et est-il seul dans cette distinction ? Alors que l’on hésite naturellement à mettre des mots dans la bouche d’une icône, l’une ou les deux choses semblent vraies : soit relativement peu de théoriciens de la réalité sont enclins à partager la vision du monde très étendue de Wheeler, soit relativement peu de théoriciens de la réalité sont capables de comprendre cette vision du monde et poursuivre ses implications. Par conséquent, malgré l’éminence de Wheeler en tant que physicien, la sienne a presque semblé être une voix dans le désert, laissant à certains l’impression que ses spéculations les plus profondes avaient plus l’air de lointaines prophéties que de pratiques théoriques immédiates. Mais si les questions, les « non » et les indices aux termes desquels Wheeler décrit sa vision peuvent parfois sembler plus lourds en intuition et en créativité qu’en rigueur logique et mathématique, ils ne sont qu’une sorte de distillations intuitives de la perspicacité mathématique que l’on pourrait attendre de quelqu’un de si expérimenté dans le raisonnement logique et quantitatif. En conjonction avec d’autres principes nécessaires, ils peuvent être transformés en propriétés logico-mathématiques de la réalité avec suffisamment de pouvoir restrictif parmi eux pour déterminer une nouvelle structure mathématique appelée SCSPL, le « langage intrinsèque » ultime. En fin de compte, il existe d’excellentes raisons de croire que cette structure est unique et que tout principe additionnel que le professeur Wheeler pourrait avoir eu à l’esprit peut être adapté par la CTMU aussi sûrement que par la logique elle-même.

Le CTMU et la conception intelligente

La théorie de la Conception, qui puise ses origines dans des « arguments depuis la conception » théologiques traditionnels affirmant que la nature était plus ou moins clairement conçue par une intelligence préexistante, soutient que la complexité observée des structures biologiques implique l’implication de causes intelligentes détectables de manière empirique. La Conception Intelligente, la plus récente création scientifique de la Théorie de la Conception, est un programme de recherche scientifique basé sur une recherche plus philosophiquement neutre, et donc scientifique, des exemples d’une forme claire, objective et standard de complexité biologique. Selon William Dembski, l’un des principaux porte-parole du mouvement, cela a conduit à « une théorie des origines biologiques et du développement » selon laquelle « des causes intelligentes [et détectables empiriquement] sont nécessaires pour expliquer les structures complexes et riches en informations de la biologie. » Compte tenu de la nature informationnelle de la complexité, Dembski observe que « l’information n’est pas réductible à des causes naturelles… l’origine de l’information est plus évidente dans des causes intelligentes. La Conception Intelligente devient ainsi une théorie permettant de détecter et de mesurer des informations, d’expliquer leur origine et de suivre leur flux. » 50

Une des premières choses à noter à propos de la définition ci-dessus est qu’elle associe les définitions impliquées d’intelligence, de causalité et d’information dans une plus grande mesure que ne le font la plupart des dictionnaires, indiquant en principe une définition commune à toutes. Comme toute bonne définition nécessite un modèle, on pourrait être fortement tenté d’inférer sur cette base que la CI, tel que défini ici, possède un modèle bien défini dans lequel tous les concepts qui le constituent sont liés. Il peut donc être surprenant pour beaucoup que l’objection, peut-être la plus fréquente, ou du moins la plus générale, à la CI dans la communauté intellectuelle élargie est qu’elle « n’a pas de modèle ». Selon ses détracteurs, il lui manque une interprétation du monde réel spécifiant un support fondamental capable de le soutenir ou un moyen de le réaliser. En outre, ses critiques affirment que son hypothèse centrale n’est pas seulement irréfutable, mais irréaliste et ne peut être confirmée empiriquement.

En toute justice, il convient de noter que, dans la mesure où la science a elle-même spectaculairement échoué à s’accorder sur un modèle global de réalité, ce n’est vraiment rien d’autre qu’un exercice d’hypocrisie. La science observe, relate et extrapole à partir d’observations avec ce qui s’avère souvent d’une grande efficacité, mais s’est toujours révélée incapable de justifier complètement ses réductions ou les correspondances entre ses théories et l’univers réel dans son ensemble. Bien que certains critiques prétendent qu’au-delà d’un certain point, les explications sont inutiles et futiles, ils ne parlent pas pour la science; le but même de la science est l’explication, et non des affirmations rationnellement non fondées selon lesquelles une explication sous forme fermante est « indisponible » ou « inutile ». En cherchant une explication cohérente de l’existence – une explication intégrant une phase de conception ontologique rationnelle, cohérente et donc intelligente – le programme CI est en fait parfaitement cohérent avec la science.

Cependant, être parfaitement consistant avec la science signifie simplement que quelque chose est en ligne pour un modèle, pas qu’il en ait déjà un. Il a donc été possible pour des critiques assidus de la CI de créer l’illusion, au moins pour une audience favorable, de l’avoir dans une situation de désavantage critique. Il a donc été possible pour des critiques assidus de la CI de créer l’illusion, au moins pour une audience favorable, de l’avoir mis dans une situation de désavantage critique. Ils soutiennent que si la science doit jouer un rôle déterminant dans la société, produire des prédictions spécifiques et citer ainsi des lois structurelles et dynamiques spécifiques qui expliquent de manière non triviale ses contextes d’application, la CI n’est rien de plus qu’un cheval de Troie pour l’idéologie religieuse, ne produisant aucune prédiction non triviale, et dépourvue de structure théorique. En raison du nombre d’oreilles favorables que de telles affirmations ont trouvées dans l’Académie, cette illusion s’est promue elle-même au statut d’illusion de masse auto-renforçante dans certains secteurs fermés d’esprits de la communauté intellectuelle. Evidemment, il serait à l’avantage du mouvement de la CI et de la société dans son ensemble de mettre fin à cette contagion en proposant clairement reconnaissable en tant que model.

Le problème, bien sûr, est que tant que la science en général n’a pas de modèle fondamental, il en va de même de toutes les tendances particulières de la science, y compris la Conception Intelligente. En raison du lien étroit qui existe entre la fondamentalité et la généralité, la CI ou tout autre domaine de la recherche scientifique devrait en définitive fournir à la science en général un modèle fondamental afin de s’en procurer un pour lui-même. Cela a pu amener certaines personnes, en particulier celles qui doutent de l’existence d’un modèle de réalité fondamental et stable, à supposer que la controverse sur la CI resterait strictement dans le domaine de la philosophie jusqu’à la fin des temps. Mais ce n’est pas le cas, car s’il n’y avait pas vraiment de modèle fondamental – s’il n’y avait pas de moyen de cartographier la cognition théorique sur la réalité dans son entièreté – la perception elle-même manquerait d’un fondement stable. Après tout, la perception peut être décrite comme la modélisation de la réalité objective dans la cognition et la modélisation de la cognition dans la réalité objective. La stabilité perceptuelle évidente de la réalité, dont dépendent absolument l’existence et l’efficacité de la science et de la méthodologie scientifique, constitue un témoignage inébranlable de l’existence d’un modèle fondamental de l’univers réel.

La nature générale de ce modèle peut être comprise simplement en considérant la réflexivité tautologique du terme « évident ». Tout ce qui est évident en soi se prouve (ou s’atteste) lui-même, et toute construction impliquée dans sa propre preuve est tautologique. En effet, dans la mesure où les observateurs sont réels, la perception revient à la réalité se percevant tautologiquement. Les ramifications logiques de cette déclaration sont développées dans le CTMU supertautologique, selon lequel le modèle en question coïncide logiquement et géométriquement, syntactiquement et informationnellement avec le processus de génération du modèle, c’est-à-dire avec une cognition et une perception généralisées. L’information coïncide donc avec la transduction de l’information, et la réalité est un processus d’auto-interprétation tautologique évoluant selon la grammaire SCSPL.

Le CTMU a un message méta-darwinien : l’univers évolue par auto-réplication et autosélection hologique. De plus, l’univers étant naturel, son auto-sélection équivaut à une forme cosmique de sélection naturelle. Mais, de par la nature de ce processus de sélection, il porte également la description d’auto-conception intelligente (l’univers est « intelligent », car c’est précisément ce qu’il doit être pour résoudre le problème de l’autosélection, le problème maître dont tous les problèmes inferieurs sont nécessairement formulés). Cela n’est pas surprenant, car l’intelligence elle-même est un phénomène naturel qui n’aurait jamais pu émerger chez l’homme et les animaux si elle n’était pas déjà une propriété latente du support d’émergence. Un objet ne déplace pas son support, mais l’incarne et sert donc d’expression de ses propriétés syntactiques sous-jacentes. Ce qui est bien plus surprenant et bien plus décevant, c’est le conflit idéologique auquel cela a conduit. Il semble qu’un groupe aime le terme « intelligent » mais soit indifférent ou hostile au terme « naturel », tandis que l’autre aime « naturel » mais abhorre le terme « intelligent ». De manière étrange, toute la controverse semble reposer sur une terminologie.

Bien sûr, on peut affirmer de manière crédible que l’argument va en réalité beaucoup plus loin que la sémantique… qu’il existe des différences de fond entre les deux positions. Par exemple, certains partisans de la version darwinienne radicale de la sélection naturelle insistent sur le caractère aléatoire plutôt que sur la conception pour expliquer comment de nouvelles mutations sont générées avant l’action restrictive de la sélection naturelle elle-même. Mais c’est intenable, car dans n’importe quel contexte scientifique traditionnel, « aléatoire » est synonyme d’« indétermination » ou d’« acausalité » et en fin de compte, l’acausalité signifie exactement ce qu’elle a toujours été : de la magie. C’est-à-dire que quelque chose qui existe sans cause extérieure ou intrinsèque a été selectionné et mis en place par absolument rien de nature causale, et est donc le genre de proposition de quelque-chose-du-néant favorisé, généralement par suspension volontaire d’incrédulité, par les habitués des spectacles de magie.

Inexplicablement, certains de ceux qui prennent cette position accusent néanmoins de pensée magique quiconque propose d’introduire un élément de volonté téléologique pour combler le vide causal. Ces parties pourraient objecter que, par « aléatoire », elles ne signifient pas une acausalité mais simplement une ignorance causale. Cependant, si en prenant cette position, elles entendent invoquer tardivement la causalité, ils initient une régression causale. Une telle régression peut prendre l’une des trois formes suivantes : elle peut être infinie et ouverte, elle peut se terminer par un Moteur Premier qui n’a pas lui-même d’explication causale ou elle peut former une sorte de cycle fermé doublant comme Moteur Premier et qui est mut. Mais un Moteur Premier semble avoir été exclu par hypothèse, et une régression ouverte infinie peut être exclue car son absence de syntaxe récursive stable lui rendrait impossible la formation de frontières informationnelles stables permettant de percevoir et de concevoir la réalité.

Qu’en est-il de la solution cyclique ? Si on utilise des lois pour expliquer des états, on est alors obligé d’expliquer les lois elles-mêmes. La méthodologie scientifique standard exige que les lois naturelles soient définies par les observations d’état. Si l’on prétend alors que tous les états sont par définition causés par des lois naturelles, il s’agit alors d’une circularité conduisant nécessairement à une définition mutuelle de la loi et de l’État. Si l’on objecte alors que cette circularité ne caractérise que le processus de la science, mais pas l’univers objectif qu’elle étudie, et que les lois ont en fait une priorité absolue sur les états, alors les lois elles-mêmes requièrent une explication par quelque chose d’autre que l’état. Mais cela éliminerait sûrement la seule alternative restante, à savoir la configuration en cycle fermé, et nous en arriverions encore à… de la magie.

Il s’ensuit que le processus intrinsèquement subjectif de la science ne peut pas être finalement séparé de l’univers objectif; l’univers doit s’auto-définir par raffinement croisé de syntaxe et d’état. Cela nous ramène au CTMU, qui dit que l’univers et tout ce qu’il contient évoluent finalement par auto-multiplexage et par auto-sélection. Dans le CTMU, la conception et la sélection, les côtés générateurs et restrictifs d’une même pièce de monnaie, sont des concepts doubles associés par les étapes alternées de la conspansion. L’auto-sélection de la réalité est inextricablement liée à l’auto-conception, et c’est ce processus en deux phases qui résulte dans la nature. L’évolution biologique est simplement un reflet de l’évolution de la réalité elle-même, un processus de récursion télique reflétant celui de l’univers dans son ensemble. Ainsi, lorsque les calculs de probabilité d’évolution sont extrapolés de régressivement de l’instant distribué de la création, ils aboutissent inévitablement à un fondement logique et donc significatif.

La CTMU affirme que, sur des bases logiques, la réalité comporte des phases génératives et restrictives, et que l’évolution comporte des phases génératives et restrictives qui s’expriment nécessairement en termes de celles de la réalité. Il affirme que le mécanisme méta-cybernétique de l’évolution est la récursion télique, un processus atemporel qui établit une dialectique stratifiée entre syntaxe et état, organisme et environnements, avec des niveaux mutable mutuellement consistants et invariants. Il dit que ce processus, bien que sujet à diverses formes de bruits, d’interférences et de concurrence fondés sur la liberté interne de la réalité, tend à maximiser l’utilité de l’univers et de ses habitants. Et il dit donc que l’évolution est bien plus qu’une simple dictature environnementale dans laquelle des lois inexplicables de la nature sifflent l’air tandis que la biologie danse servilement la gigue de la vie et de la mort.

La CTMU affirme que, de par sa nature auto-générative et auto-sélective, qui découle directement de l’exigence analytique de l’autonomie, la réalité est son propre « concepteur ». D’autres caractéristiques de la grammaire générative de la réalité impliquent que la réalité possède certaines propriétés logiques traditionnellement considérées comme théologiques ou spirituelles et que, dans cette mesure, l’aspect auto-conçu de la réalité est ouvert à une interprétation théologique ou spirituelle. La CTMU, en tant que théorie logique, ne tente pas de faire avaler de force une telle interprétation à qui que ce soit; toutes les permutations sémantiques ne doivent pas nécessairement affecter la structure théorique. Ce qu’il fait, cependant, rend toute interprétation anti-théologique a priori fausse et garantit que quelle que soit l’interprétation choisie, elle tienne compte de l’existence d’un « concepteur intelligent »… à savoir la réalité elle-même. À la lumière du CTMU, cette question relève désormais davantage de la logique que du goût.

Quoi qu’il en soit, il devrait être clair que le CTMU offre de nouvelles façons de considérer à la fois l’évolution et la téléologie. Tout comme elle se distingue d’autres théories de l’évolution cosmique par son degré d’autonomie, en particulier en ce qui concerne sa préférence pour l’autodétermination plutôt que pour la détermination externe ou l’indétermination, il en va de même pour son approche de l’évolution biologique. Contrairement aux autres théories, le CTMU place carrément la biologie évolutionnaire dans un contexte de modèle de réalité fondamental et autonome, lui fournissant ainsi une explication et un fondement qui lui sont propres au lieu de passer de façon irresponsable à une réduction future; au lieu de la juger suffisante pour modéliser ses implications évolutives dans le monde biologique, le CTMU établit une symétrie théorie modèle en fournissant un mélange homogène de théorie et d’univers dans lequel le monde biologique peut lui-même être « modélisé » par incorporation physique. Rien que cela lui donne une place dans le débat sur l’évolution.

Remerciements

L’auteur souhaite remercier Gina Lynne LoSasso pour la création des diagrammes qui apparaissent dans ce document et pour les nombreuses discussions et commentaires stimulants concernant la présentation de ce travail. Un grand merci également à un certain nombre de personnes qui ont soutenu et suivi mon travail et contribué à des questions stimulantes qui m’ont aidé à expliquer le CTMU dans son niveau de détail actuel. Ceux-ci incluent, entre autres, Robert North Seitz, John Chapman, Angell O. de la Sierra, Mike Doyle, Phillip Hopp, Quinn Tyler Jackson, Evangelos Katsiolis, Paul Kisak et Anthony Nolan.

© 2002 Christopher Michael Langan. Consultez la version la plus récente de cet article sur : hology.org

Notes

1 David Berlinski, « What Brings a World into Being? », Commentary, Vol. 111, No. 4, 2001, p. 17.

2 Robert H. Wozniak, « Mind and Body: René Descartes to William James », https://serendipstudio.org/Mind/, 1996.

3 Michael J. Behe, Darwin’s Black Box, New York: Touchstone Books, 1998.

4 William A. Dembski, The Design Inference: Eliminating Chance through Small Probabilities, Cambridge University Press, 1998.

5 En fait, ils sont identiques jusqu’à un isomorphisme au-delà duquel le côté mental, le plus complet des deux, dépasse le matériel.

6 Bien que le CTMU soit par définition unique en son genre jusqu’à l’isomorphisme avec sa propre syntaxe – cet « auto-isomorphisme » est l’une de ses caractéristiques structurelles définitives – nous nous abstiendrons d’écarter sommairement la possibilité qu’à l’avenir, d’autres puissent présenter des « Modèles de rétroaction temporelle » auto-déterminantes propres. Il convient toutefois de noter que, étant donné que le CTMU est intrinsèquement tautologique et identifiée tautologiquement avec son univers au niveau le plus profond de son existence, et puisqu’il s’agit du même univers réel étudié par la science, toute autre théorie valide de la réalité équivaudra nécessairement au CTMU jusqu›à l›isomorphisme; quoi qu’il ajoute par spécificité, non par généralité. Bien que d’autres aient déjà présenté des théories « cybernétiques » et « théories de l’information » de la cosmologie, ces théories reposent sur les théories standard de l’information et de la cybernétique et héritent donc de leurs limitations explicatives vis-à-vis de la cosmologie.

7 Ceux qui s’attendent à ce que le champ de la cosmologie aboutisse à une grande réduction de l’univers à de l’information pure oublient parfois que cela transformerait simplement une certaine question, « Qu’est-ce que l’univers et d’où vient-il ? », en une autre question non moins épineuse, « Qu’est-ce qu’une information et d’où vient-elle ? »

8 John A. Wheeler, « Beyond the Black Hole », dans Some Strangeness in the Proportion: A Centennial Symposium to Celebrate the Achievements of Albert Einstein, Woolf, H. (Ed.), pp. 341-375, Reading, Massachusetts : Addison-Welsley, 1980, pp. 341-375.

9 John A. Wheeler, « Information, Physics, Quantum: The Search for Links », p. 8, dans Complexity, Entropy and the Physics of Information, SFI Studies in the Sciences of Complexity, vol. VIII, Zurek, W.H. (Ed.), Addison-Wesley, 1990, pp. 3-28.

10 « From the Big Bang to the Big Crunch », entretien avec John A. Wheeler dans Cosmic Search Magazine, Vol. 1, No. 4, 1979. Voir : http://www.bigear.org/vol1no4/wheeler.htm

11 ibid.

12 Wheeler, « Information, Physics, Quantum », pp. 3-4.

13 ibid., p. 3.

14 ibid., p. 4.

15 ibid., p. 8.

16 ibid., p. 9.

17 ibid., p. 9.

18 ibid., p. 10.

19 ibid., p. 10.

20 John A. Wheeler, Gravity and Spacetime, New York: Scientific American Library, 1990, ch. 6.

21 Wheeler, « Information, Physics, Quantum », p. 15.

22 ibid., p. 16.

23 Nous allons ignorer pour le moment le fait que si l’esprit est illusoire, il en va de même de toute philosophie, y compris celle de Hume, et si la causalité est illusoire, il en est de même de la forme de causalité représentée par implication logique, y compris l’utilisation par Hume de l’implication logique pour définir sa philosophie.

24 Bertrand Russell, History of Western Philosophy, London : Unwin Paperbacks, 1979.

25 Christopher M. Langan, « Of Trees, Quads, and God », Noesis-E, Vol. 1, No. 4, 2001.

26 Kurt Gödel, On Formally Undecidable Propositions of Principia Mathematica and Related Systems. Meltzer, B., transl., New York : Basic Books, 1962.

27 Pour plus d’informations sur le théorème de Lowenheim-Skolem et la thèse de Duhem-Quine, voir Christopher M. Langan, « The Theory of Theories », Noesis-E, Vol. 2., n ° 1, 2002.

28 L’interprétation Many Worlds de la mécanique quantique, en prétendant contourner le problème de l’effondrement de la fonction d’onde de la mécanique quantique, prétend en fait contourner également le problème de la conscience divisée. Cependant, puisque le MW est lui-même nécessairement formulé en termes de logique bi-valuée, le problème régresse de la même manière que « l’hyperunivers » associé au MW « s’effondre » lui-même hors de la mer de toutes les « méta-réalités » potentielles. Sur ce point, le MW a peu d’éclairage à offrir pour son propre compte. Le MW manque donc d’autonomie justificative et n’est donc pas une base pour une théorie fondamentale de la réalité. Quoi qu’il en soit, puisque la théorie que nous décrivons dans le présent document est conçue pour aborder la réalité dans sa forme la plus fondamentale, et donc pour traiter toutes les réalités concevables comme ses instanciations possibles, elle supplante toute explication fournie par le MW seul.

29 Il y a plusieurs millénaires, Aristote a proposé la logique (catégorique) comme règles formelles du raisonnement correct. Maintenant comme alors, le « raisonnement » est de nature inférentielle, mentale et subjective. Après avoir été en grande partie immobile jusqu’au XIXe siècle, le champ de la logique a commencé à connaître de nouveaux progrès. Mais, bien que ces progrès aient été considérables, ils ont laissé essentiellement intactes la nature inférentielle, mentale et subjective de la logique.

30 Ces principes sont en réalité assez étroitement liés dans le sens où ils peuvent dans une certaine mesure être déduits les uns des autres dans un contexte de réalité théorique.

31 En physique, l’expression « Principe de Réalité » a parfois été associée à l’idée que la réalité objective existe indépendamment de l’observation humaine, au moins dans la mesure où elle ne disparaît pas soudainement si elle n’est pas surveillée directement. Tel qu’utilisé dans le présent document, l’expression « Principe de Réalité » doit être interprétée de la manière décrite dans la présente section, sauf indication contraire.

32 Remarque: la résolution type-théorique de ce paradoxe est incomplète; La résolution complète nécessite le MU, une sorte de « méta-syndifféonèse » conférant au réseau infocognitif de l’espace-temps un niveau de fermeture supérieur.

33 Une régression syndifféonique conduit ultimement à une syntaxe fermée stable dans laquelle tous les termes sont mutuellement définis; La définition mutuelle est ce qui stabilise et confère au système une déterminabilité interne (identifiabilité interne des événements) par le biais de la symétrie syntactique. En d’autres termes, la fermeture relationnelle orthogonale à la dimension (temporelle) de la régression équivaut à la distribution d’une identité systémique et, à moins que cette identité soit complètement définie, les identités des composants du système ne peuvent être définies ou reconnues les unes par rapport aux autres. Ainsi, l’identité dynamique est une fonction d’auto-identification avec des dimensions définitives, descriptives et interprétatives.

34 Il est tentant de noter que « relativité » signifie à peu près la même chose dans la Théorie Générale de la Relativité que dans le cas présent. C’est-à-dire qu’en utilisant un « espace tangent » à syntaxe distribuée, la structure de l’espace-temps est définie tensoriellement en termes de masses et de positions relatives de son propre contenu matériel, ce qui résulte en une définition intrinsèque de l’espace-temps de type MAP. Malheureusement, le formalisme de base de la RG, la géométrie différentielle, n’est pas autonome par rapport au temps; dans sa formulation actuelle, il s’appuie tacitement sur un support d’inclusion (conspansif) pour lui donner un potentiel temporel.

35 Ce qu’une telle question demande vraiment est « pourquoi la relation d’habitat et d’observation se tenant entre l’observateur/questionneur et l’univers existe ? » Le Principe Anthropique Faible va à mi-chemin vers une réponse en appliquant une fonction de sélection probabiliste : « La relation a été sélectionnée logiquement par le fait que seuls certains types d’univers peuvent accueillir des actes d’observation et un observateur comme le questionneur. » C’est juste jusque-là, mais cela omet la phase générative, présélective de l’explication… la partie qui représente la fonction de sélection et le domaine auquel elle s’applique. À cet égard, le PAF ressemble un peu à la sélection naturelle; il verdi assez bien le jardin, mais est incapable de faire pousser une seule fleur.

36 Notez que le Principe M = R n’affirme pas (par exemple) que les fruits de l’imagination humaine sont « réels » sauf en tant que schémas de déclenchement neuronaux sans lien nécessaire avec quoi que ce soit en dehors du cerveau, ou que nous pouvons immédiatement rendre les choses « réelles » simplement en pensant à elles. Le Principe M = R dit simplement que, lorsque l’esprit est le moteur de la cognition et de la perception, et que ces processus sont considérés conjointement comme un « langage » obéissant à des règles de syntaxe, cette syntaxe – les règles de la cognition et de la perception – se distribue nécessairement sur le percepteur et la perception.

37 Christopher M. Langan, « Introduction to the CTMU », Ubiquity, Vo.1, No.1, 1999.

38 Arthur S. Eddington, The Expanding Universe, Cambridge University Press, 1933.

39 Christopher M. Langan, « Physics and Metaphysics », Noesis-E, Vol. 1, No. 3, 2001.

40 Un processus de Markoff est un processus stochastique sans mémoire. En d’autres termes, il s’agit d’un processus répondant à deux critères: (1) les transitions d’état sont contraintes ou influencées par l’état actuel, mais pas par la séquence particulière des étapes menant à l’état actuel; (2) la transition d’état contient un élément de hasard. Les processus physiques sont généralement supposés répondre à ces critères; les lois de la physique sont définies conformément à 1 et, puisqu’elles fonctionnent ultimement au niveau quantique mais ne déterminent pas totalement les transitions d’état quantique, un élément de hasard est présent superficiellement. C’est dans ce sens que les lois de la physique distribuées peuvent être appelées « markoviennes ». Cependant, le critère 2 ouvre la possibilité que des influences cachées soient actives.

41 Christopher M. Langan, The Art of Knowing: Expositions on Free Will and Selected Essays, Eastport, NY : Mega Foundation Press, 2002.

42 Gellert, W., Kustner, H., Hellwich, M., and Kastner, H., The VNR Concise Encyclopedia of Mathematics, New York : Van Nostrand Reinhold Company, 1977, p.334.

43 Toutes les expressions ne sont pas des propositions; les propositions sont des expressions sans variables libres (non quantifiées). Permettre la quantification des prédicats unaires (un lieu) et les traiter comme des individus aboutit à une généralisation des langues élémentaires à une classe de langues plus expressive, les langues monadiques du second ordre. D’autres généralisations sont possibles dans ce sens.

44 Si l’inclusion de l’utilité, des qualias ou des sentiments semblent « non scientifique », il suffit d’observer qu’il serait beaucoup plus non scientifique d’ignorer des choses que l’on sait subjectivement exister selon l’hypothèse souhaitée et rationnellement injustifiable que la subjectivité et les prédicats subjectifs ne jouent aucun rôle dans l’auto-définition de la réalité. Dans la mesure où la subjectivité fait simplement référence aux identités intrinsèques cohérentes des éléments de relations objectives, ce serait logiquement absurde. Quoi qu’il en soit, notre objectif à ce stade est simplement de classer les éléments de base en fonction desquels nous voyons le monde, qu’ils aient été prouvés ou non accessibles à la méthodologie empirique standard, et cela implique de reconnaître la réalité des prédicats qualiques et émotionnels et de joindre les constantes non logiques correspondantes à la syntaxe SCSPL. Si les prédicats SQP et SET s’avèrent réductibles à des prédicats plus fondamentaux SETO/SLM, alors très bien; cela permettra une réduction commode de la syntaxe. Mais ce n’est certainement pas quelque chose qui peut être décidé à l’avance.

45 La syntaxe cognitive-perceptuelle comprend (1) des ensembles, sur-ensembles ou sous-ensembles d’attributs (télons), (2) des règles perceptuelles d’attribution externe pour la mise en correspondance de relations externes en télons, (3) règles cognitives d’attribution interne pour la transition d’état cognitive (interne, non perceptuelle), et (4) les lois de dépendance et de conjugaison selon lesquelles des règles perceptuelles ou cognitives d’attribution externe ou interne peuvent ou non agir dans un ordre particulier ou de manière simultanée.

46 Pour voir comment l’information peut être réduite de manière bénéfique lorsque, par définition, toutes les informations sont non informatives, il suffit de reconnaître qu’elles ne constituent pas une proposition autonome; elle ne se trouve jamais en dehors de la syntaxe. En effet, ce n’est que par acquisition syntactique que quelque chose est toujours « trouvé ». Ce qui n’est reconnaissable que comme contenu syntactique nécessite un confinement syntactique, ne devenant significatif que s’il est acquis par un opérateur syntactique capable de maintenir sa structure relationnelle; sans transduction attributive, un bit d’information n’a rien à quantifier. Cela implique que l’information puisse être généralisée en termes de « ce qu’elle a en commun avec la syntaxe », à savoir la relation syndifféonique entre information et syntaxe.

47 Aux fins actuelles, la réduction peut être comprise comme une production inversée. En tant que tel, il est essentiel à la reconnaissance grammaticale.

48 Parce que la propagation de la lumière est un phénomène dépendant de la conspansion, c ne peut pas être affecté par l’impédance ou la manipulation de photons.

49 L’Ordre Impliqué est un concept défendu par le regretté physicien David Bohm en rapport avec son interprétation de la mécanique quantique. En utilisant l’analogie d’un hologramme, Bohm a proposé une espèce d’auto-similarité dans laquelle « tout est enveloppé dans tout ». Selon Bohm, cet « ordre impliqué » est complémentaire d’un « ordre expliqué », le résultat de son déploiement via un processus appelé « holomouvement ». Cela mérite d’être mentionné en raison de sa ressemblance superficielle avec le déploiement conspansif de l’état à partir de la syntaxe dans le SCSPL, qui affiche sa propre version de l’hyperconnectivité logique, et de la similitude entre hologie et holographie. Cependant, étant donné que le CTMU ne recoupe que partiellement la théorie de Bohm, l’analogie ne doit pas être trop étendue.

50 William A. Dembski, « Intelligent Design as a Theory of Information », Perspectives on Science and Christian Faith, Vol. 49, No. 3, 1997, pp. 180–190.

Dernière révision de la traduction le 02/09/2024.

Contenus

CTMU-FR.COM © 2024 par CTMU-FR est sous licence CC BY-SA 4.0